伝達方程式
最も簡単な波動方程式ー伝達方程式を解いてみましょう. 2変数関数\(u(t,x)\)が次の式を満たすとします:
\[\frac{\partial u}{\partial t}+c\frac{\partial u}{\partial x}=0\]
なお偏導関数も2変数関数なので, \[\frac{\partial u}{\partial t}(t,x)+c\frac{\partial u}{\partial x}(t,x)=0\tag{1}\]という意味ですよ. これは, ある曲線\[\frac{\text{d}X(t)}{\text{d}t}=c\]つまり\[X(t)=ct+x_0\]に沿っての\(u(t,x)\)の方向微分, つまり関数値\(u(t,X(t))\) (これは\(t\)だけの関数ですね)の変化を考えると,
\[\frac{\text{d}u(t,X(t))}{\text{d}t}=\frac{\partial u}{\partial t}(t,X(t))+\frac{\partial u}{\partial x}(t,X(t))\frac{\text{d}X(t)}{\text{d}t}=0\](最後0になるのは,(1)で\(x\to X(t)\)を代入したのだ )となることから, 解は\[u(t,X(t))=\text{Const.}\]となることがわかります. この曲線(今は直線か・・・)を特性曲線と呼びます. 例えば\(t=0\)で初期値\(f(x)\)が与えられているのであれば, \[u(0,X(0))=u(0,x_0)=f(x_0)\]であり, これが時間によらないので\[u(t,X(t))=f(x_0)=f(X(t)-ct)\]が成り立ちます.\(xt\)平面を特性曲線が埋め尽くしているので, \(t,x\)を独立変数と考えると, \[u(t,x)=f(x-ct)\]が解です.
陽的差分法
差分法でこれを解いてみましょう.空間\(x\)及び時間\(t\)を, 整数\(n,i\)を用いて以下のように離散化します:\[t_n=n\Delta t,\quad x_i=i\Delta x\]. 差分法では, この格子上の値\[ u_i^{(n)}=u(t_n,x_i)\]の変化について差分式を考え, それを解いて解を求めます.
差分法で用いる格子点の選択は重要です.
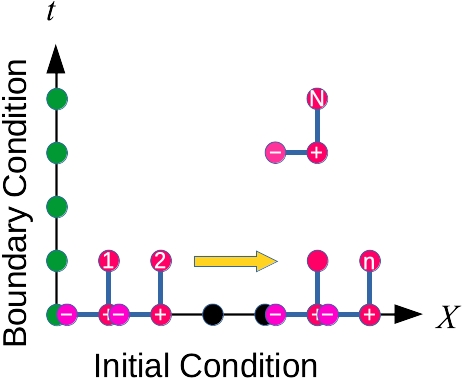
図の右上の3点を用いると, 時間微分と空間微分が差分近似できる:\[\frac{\partial u}{\partial t}\sim\frac{u_N-u_+}{\Delta t}\]\[\frac{\partial u}{\partial x}\sim\frac{u_+-u_-}{\Delta x}\]これを用いると,差分式\[\frac{u_N-u_+}{\Delta t}+c\frac{u_+-u_-}{\Delta x}=0\]が得られるので, これを解くと\[u_N=(1-K)u_+ +K u_-,\quad K=\frac{c\Delta t}{\Delta x}\]
これを用いると, \(n=1\)のデータを図の1,2,...の順に求めていくことができます. \(n=1\)のデータがわかれば, \(n=2\)がわかる・・・
こうして,時間発展を追うことができます. \(u_N\)が全て既知の値で表されている点に注目して,陽的差分法(explicit scheme )と呼びます.
時間発展を追う問題では, 初心者の想像とは異なり, 時間\(t\)の方向に配列を用意することはありません.1層づつ解いていくので, 例えば\(n=10\)を解くときには, 既に\(n=1,2,\ldots, 8\)くらいまでは全く関係がなくなっています.もちろん時間方向の配列を用意できるなら用意すれば良いのですが,それでは,時間配列を用いない同業他者様は, 同じメモリーサイズを用いて,ずっと細かい空間格子で計算してしまう(つまり競争に負ける)からです.
だいたいは,こんな感じのプログラムになるでしょう:
こたえ
こんな感じ:
// main.cpp
#include <iostream>
#include "CONV.hpp"
int main()
{
size_t nx=100; // 空間分割数
double dt=0.01; // 時間刻み幅
size_t ntmax=1000; // 最大時間ステップ数
size_t ntsave=10; // データ保存間隔
CONV mySolver(nx,dt,"Data/pde100.data");
mySolver.Write(); //初期値も保存しよう
for(size_t nt=0;nt<ntmax;nt++)
{
mySolver.Step();
if (nt % ntsave == 0) mySolver.Write();
}
return 0;
}
これで,作成すべき CONV クラスの仕様が定まりました.
- CONVクラスは, 空間格子点数nx, 時間ステップ dt, 出力ファイル名を与えて初期化する. ここで初期分布も作成する
- CONV::Write()関数は, 現在の時刻の分布をファイルに書き出すべきである
- CONV::Step()関数は, 時間ステップが一つ進む
まあ変更もあるかもだが,実装しながら解説:
先頭部分( まずは自分で書いてから,ね)
定義の読み込みと, メンバー変数のところは:
// CONV.hpp
#pragma once #include <iostream> #include <filesystem> #include <cmath> #include <vector> #include <fstream> class CONV { double dt, CFL; double time; class Point //めんどくさかったので, 内部クラスにした { public: size_t id; // これは・・・いらないかもな? double X; double U_VAL; // U_n double U_PRE; // U_{n-1} }; std::vector<Point> Data; std::ofstream ofs;
コンストラクタは, 保存するファイル名を入れて初期化する予定でしたが.なーんか,それ本質じゃ無い気がしてきて
- ほれ.コンストラクタは「最初にやること」ですよね.できたファイルを保存する名前,は,そうじゃ無い気が
- むしろ「初期値を指定する」のが良いのでは無いか?とおもったので, 仕様を変更.ラムダ式で与えても良いが,忘れるユーザの対策もしておいた
public: CONV(const size_t& nx, const double& dt, const std::function<double(double)>& U0 = [](double x) { return 0.; }) : dt(dt) { double xmax = 1.0; time = 0.0; // 初期時間 double dx = xmax / nx; // 空間刻み幅の計算 CFL = dt / dx; // CFL条件の計算 Data.resize(nx + 1); // 空間分割数に基づいて初期化 for (size_t i = 0; i < Data.size(); ++i) Data[i].id = i; // 各点のIDを設定 for (auto& P:Data) P.U_PRE = P.U_VAL = U0(P.X = P.id * dx); // 初期条件の適用 std::cout << "Starting CONV solver with nx=" << Data.size() << ", dt=" << dt << std::endl; }
おや.ここいらへんの const とは,なんでしょう? それは後で説明しますね!
Write()の 実装
書き出しファイル名は, Write()を最初に呼び出すときに与え, それ以外では引数なしにしましょう.
bool Write(const std::string& filename)
{
if (ofs) ofs.close(); // 既存のファイルストリームを閉じる
std::filesystem::path datafile = getenv("HOME");
datafile /= filename; // 引数のファイル名は,$HOME に相対的なモニに限定
std::filesystem::create_directories(datafile.parent_path());
ofs.open(datafile);
if (!ofs) throw std::ios_base::failure("Failed to open file: " + datafile.string());
return Write(); // 引数なし版: 現在のofsにデータを書き出す
}
bool Write()
const {
try
{
ofs << std::endl << "# time= " << time << std::endl;
for (auto &v : Data) ofs << v.X << " " << v.U_VAL << std::endl;
}
catch (const std::exception &e)
{
std::cerr << "Error writing to file: " << e.what() << std::endl;
return false;
}
return true;
}Step()
Stepはスキーム通りです. Step()の引数に,境界条件の該当時刻の値を与える,という仕様訂正をしました.
void Step(const double U_W=1.0) { time+=dt; Data[0].U_VAL = U_W; for(size_t i=1;i<Data.size();++i) Data[i].U_VAL=(1.-CFL)*Data[i].U_PRE + CFL*Data[i-1].U_PRE; for(auto& v:Data) v.U_PRE=v.U_VAL; }
double get_time() const { return time; }
数値計算的には, この辺で, 計算した分布を, 以前の分布として交換するのを忘れるとまずいですよね!この関数の意味は,後で説明しますね!
constってなに?
「定数ですねん」と宣言することです.主に4種類
- 変数がconstである
- 最近のコンピュータのメインメモリーは(CPUに比べて)遅いです.
- 「ここの値が欲しい」とメモリーに伝えてから,実際にゲットするまで,30回分の計算回数(クロック)を使ったりします.
- すると,こんなことが起こります:
- 昔々,あるメインメモリーに,ある変数の値がありました.
- CPUに住んでいた,ある関数が, const指定なしで,その変数を利用したいと思いました!
- コンピュータは,えっちらおっちら,メインメモリーから値を読み出し, CPUに運びました(30回待ち)
- 使っただけで変数の値は変更しなかったのですが,コンピュータには,その事実が確認できませんでした.
- 仕方がないので,その変数の値を,えっちらおっちら,メインメモリーに書き戻すことにしました(30回待ち)
- CPUは暇になってしまいましたが,その変数がメインメモリーに書き込まれるまで,次の手が打てませんでした.
- const指定をしていると,
- コンピュータは,えっちらおっちら,メインメモリーから値を読み出し, CPUに運びました(30回待ち)
- 関数は終わりました.その変数は変更されてないので,ポイしました.
- CPUは,直ちに,次の仕事を始めました
- 後者の方が,この作業の分だけ早いですよね.まあでも前者のこの作業があるから,せいぜい2倍速だろ,というと,そうではないです.
- 最近のCPUは,「この野郎は,近い将来60%程度の確率でこの作業が必要になるはず」
- だから60%のCPUコアは,博打でこの作業を実際より先に行なっておけば30回待たずにすむ,などと勝負をかけています.なので,もう少し早くなります.
- ま,正直,変数がconstなのはconstと書いた方が,実感的にはかなり高速になります.
- なので, ここに来るまでの間にAIモンキーが出力するコードに,やたらとconstと書いてあるのに気付いた人は多いでしょう.
- とりあえず問題が起こるまではconstしまくった方が良い,ということではないでしょうか.
- 関数の引数がconst &である
- 上の例のように,関数の引数が
const Type &となっているケースは多い. - まず, & がついていない関数呼び出し
function(myClass X)では,何が起こるかといえば- &の付いていない引数は,コピーしてから関数で利用します.
- これは契約ですので,Xが1GBのメモリーを使うなら,必ず1GBのコピーをしてから使います.
- おそいやん・・・
- そこで型名Typeに参照&を付けます.
function(myClass & X)ですね.同じ物体Xを使うので,コピーは起こりません. - でも今度は,そのXが変更されるかもしれないという心配が出るので,メインメモリーへの書き戻しは必要ですね.
- そこで
const Type &です!メインメモリーから読み出しonlyでコピーなし,使用後に破棄決定で,これが一番無駄が少ない.
- 上の例のように,関数の引数が
-
関数の戻り値がconst &である
- 関数が
const Type& function(...)と宣言されている場合です.これなら,function()が500GBのデータを作って返却しようとしても, コピーは起こりません const Type& VALUE=function(...)としてVALUEの値を利用できます.VALUEの値は変更できないです(だって,定数だもん!)- 昔は, function()が大きなデータを戻り値にするには,コピーが発生しないように,この書き方をしていました.
- まあconstにしないで,
Type& function(...)が書けるのなら,それでいいんだけれども,実際には下に述べる事情でwwwとなってしまうことがある - が,時代は進み,最近のC++コンパイラーはReturnValueOptimization技(略してNRVOの秘技. 最初のNについては, 今はヒ・ミ・ツ)というのを持っていて,無駄コピーを自動で省きます.
- なので,まあ,書き方は変わっていくのではないかな
- まあconstにしないで,
- 関数が
- 関数がconstである
const Type& VALUE=function(...)として作り出したクラスは,自分の状態を変更できないです(だって,定数だもん!). すると,いろいろな縛りが出てきます.- あなたは, Typeクラスに関数Type.myFunc()が付いているので,VALUE.myFunc()しようとしました.ところが, 「おまえ,Typeはそうではないが, VALUEはConstであるぞ.Type.myFunc()は自分の状態を変更する可能性があるから,呼んじゃダメだよん」となってしまう.
- そこで登場するのがconst関数です.自分の状態を変更しない,良い子ですよ,と宣言するのです. ここで定義している get_time() 関数のように書きます.
- じゃ,関数全部に const 付けときゃ良いじゃん,と思うかもしれませんが,最近のC++コンパイラを舐めてはいけません.
- 関数内部でメンバー変数を変更していると,文句を言われます(←そりゃ堂々とやりすぎじゃろ)
- メンバー変数に
std::vectorがあって, そいつをresize()しててもダメ. - 出力ファイル
std::ofstreamに << なんか書いちゃった,もみつかります. std::map<....> Mが含まれていて,M[ key]にアクセスしてもダメです.M[key]が既に存在したとしても,std::map[]は「keyが定義されてなければ作成」する仕様だからです.M.at(key)はOKです(keyが定義されてなければ自爆する仕様なので)
実行してみる
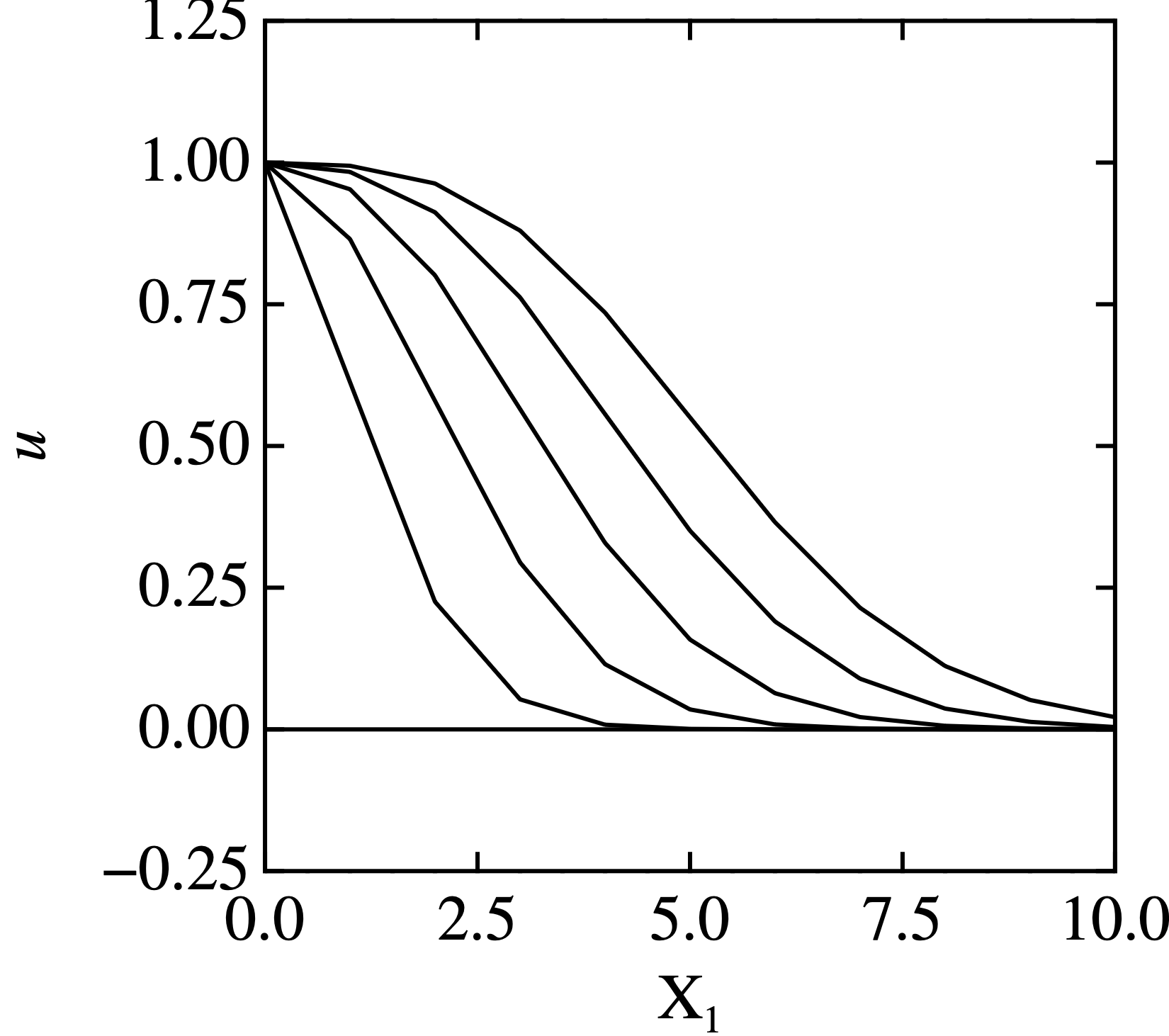
xmax=10, \(\Delta t=0.1, N_x=10\), ntmax=50 で実行してみました!初期値はデフォルトの\(u=0\)で,境界条件は\(u=1\)です.
myMac[data]$ graph -Tps -C --line-width 0.003 -y -0.25 1.25 PDE_01.dat |ps2pdf -dEPSCrop - new.pdfで作図すると,
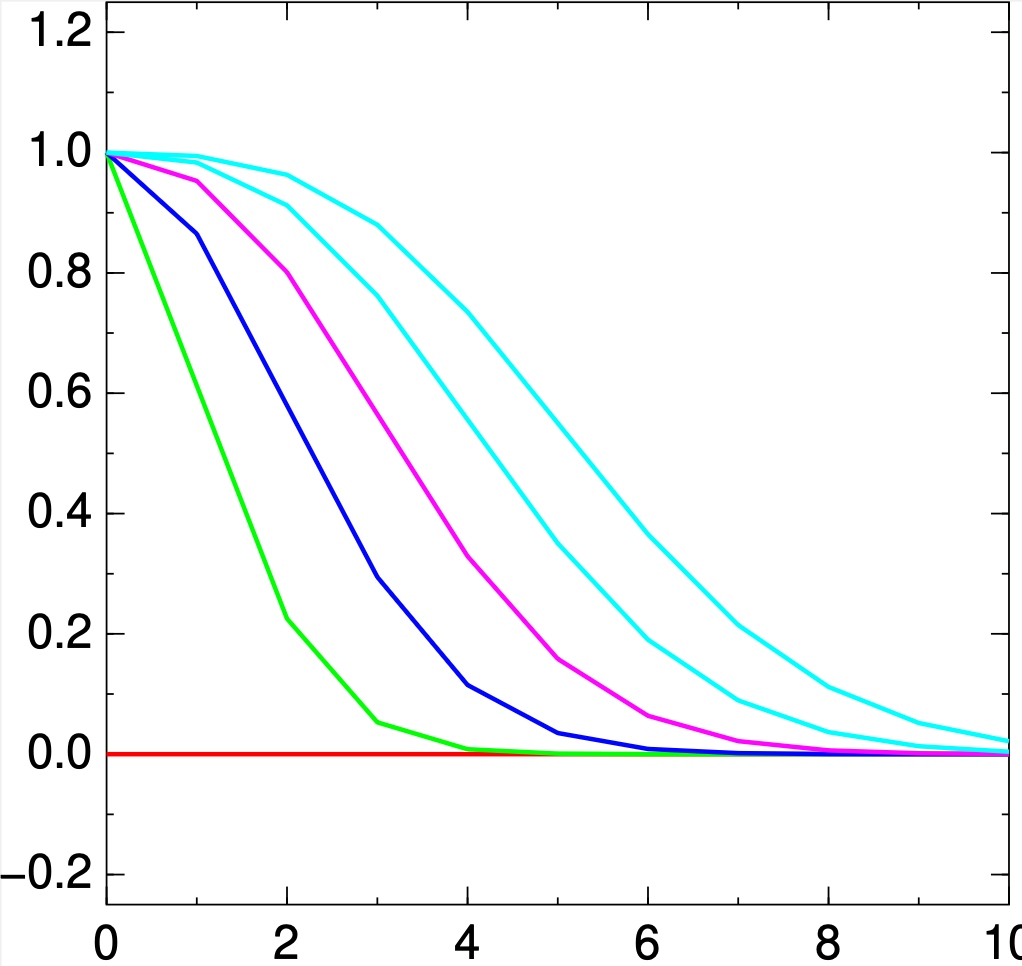
なんか,ダレまくっているな.厳密解は数学で学んだが,たしか\[u=\cases{1&($x<ct$)\\0&($x>ct$)}\]でしたよね・・・
皆さんの仕事は,これをもう少しマシに解くことです.
プログラムが動くようになったら,以下の検討を行ってみてください:
- 変数CFLの値\[C=\dfrac{c\Delta_t}{\Delta_x}\tag{2}\]をCourant-Friedrichs-Lewy (CFL)数という. この解法は, CFL < 1 の場合にしか利用できない.
- CFL > 1 では何が起こるか,確かめてみよ.
- CFLを色々に変えて, 厳密解と比較してみよ.
- \(\Delta t, \Delta x\)を小さくすると厳密解に近づくのか?
- 差分式\(u_N=(1-K)u_+ +K u_-\)は内挿・外挿の公式のような気がする. どのような内挿・外挿であるか, 考えてみよ.
- 初期値が滑らかな関数である場合, 初期値が不連続な関数である場合について, 計算を行ってみよ.
- \(\Delta x, \Delta t\)をさまざまに変え, 誤差がどの程度であるか調べてみよ.
- \(c>0\)の場合, 下図の差分では, 全く解けないことを確かめよ. \(c<0\)の場合には, どうか?
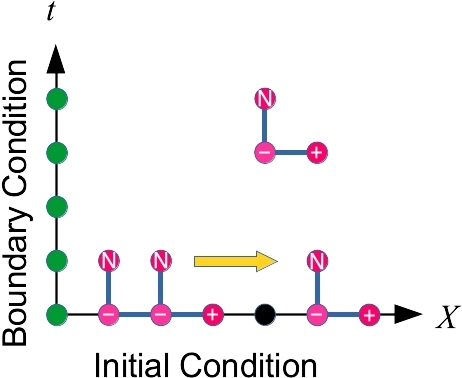
- 研究においては,上の挿絵のようなものを描く必要がある.描けるようになっておけ.
draw.shで作図
やはり厳密解と比較した図が作りたいな,なんてのが簡単なのが,draw.sh の利用ですね.PlotUtilsをインストールしているのなら,ダウンロードするだけで使えます:
myMac[data]$ git clone https://bitbucket.org/sugimoto605/draw.git myMac[data]$ cp draw/draw.sh . myMac[data]$ cp draw/standards.sh . myMac[data]$ ./draw.sh -i
これで,サンプルプログラム my.sh が作成されます.あなたは2度と draw.sh とタイプして実行することはないです.あなたが実行するのは my.sh です.実行してみましょう.
myMac[data]$ ./my.shこれでサンプル my.pdf ができます(左の図):
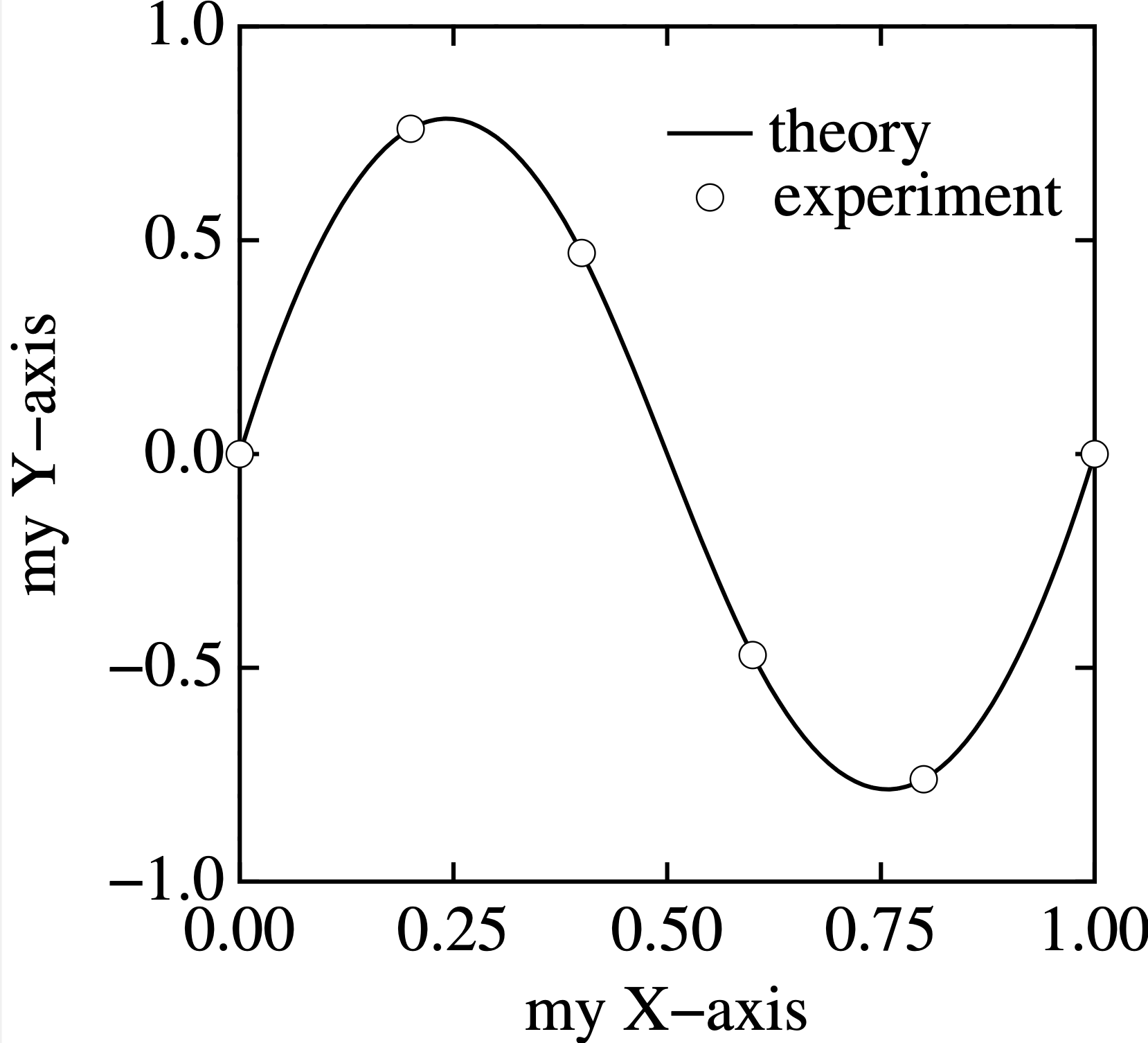
では, my.sh を変更して,自分の思う図を描きましょう:
#!/bin/bash . draw.sh . standards.sh ←これは入れた方が楽 COLOR=1 ←現代では標準がカラーの図だよね? X_AXIS='X\sb1\eb' ←X軸の表題. \sb....\ebの間は添字 X_RANGE='0 10 2.5' ←みたらわかるやろ,X軸の範囲と目盛間隔 Y_AXIS='\fIu' ←\fI と打つとイタリック文字 Y_RANGE='-0.25 1.25 0.25' LINE=( Solid:Black Solid:Red Solid:Blue Solid:Magenta Solid:Cyan ) ←1番目のファイルの色,2番目のファイルの色.. SYMBOL=( Omit ) ←1番目のファイルのマーカー・・・ cat > $TMP/legend.dat <<@ @ LEGEND=$TMP/legend.dat draw my.pdf おまえさんのデータファイル
このソフトは,色を変更するには別のファイルにしないとですね!ま,それは後で学ぶとして,謎のlegend.datですが,ようするにオマケのデータファイルをここで書けます. 例えば
cat > $TMP/legend.dat<<@ #analytical solution t=1 ←解析解のデータを自分で書いちゃえ #m=Dash:Red,S=Omit ←データファイルに,こう書けば,色を変えられるのじゃ 0 1 1 1 1 0 10 0 ←お約束の,空行で線切り替え #analytical solution t=2 #m=Dot:Blue,S=Omit 0 1 2 1 2 0 10 0 #m=Solid:Black,S=Omit ←じつは#でも線切り替え 3.25 0.5 5.0 1.0 lb:\fIt=3 ←1980年のソフトなので,日本語は入れられないです @
これで,下の絵が描けます.手っ取り早いんだよね,これ. my.sh も使いまわせるしなあ. あ?引き出し線のここの数値はなんやってか?そんなもん,テキトーに見えるように描いたらええんや.どうせ,人間が読むんやから.
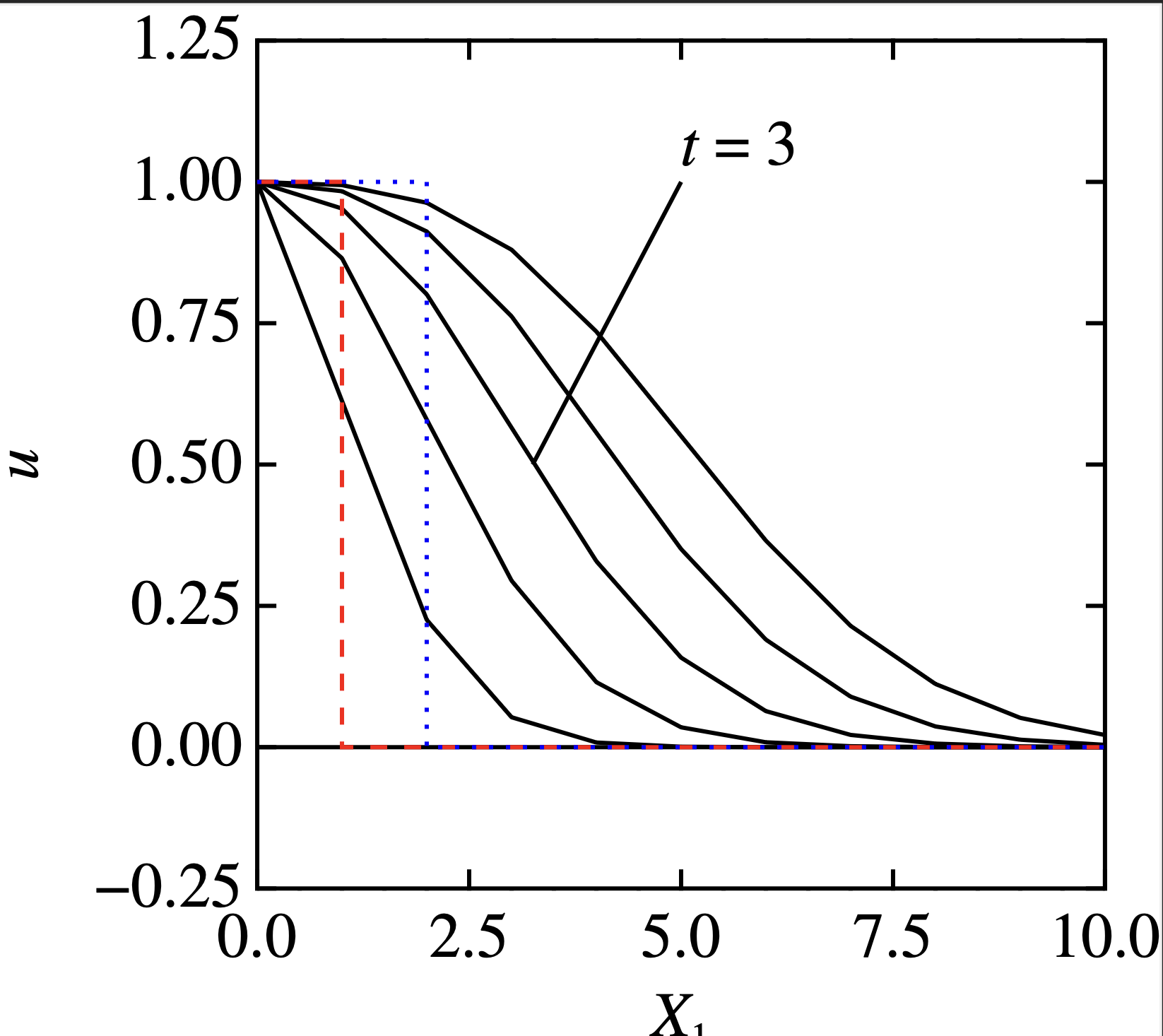 日本語をどうしても入れる場合は, libreOffice/Drawで好きに入れちゃってくださいな:
日本語をどうしても入れる場合は, libreOffice/Drawで好きに入れちゃってくださいな:
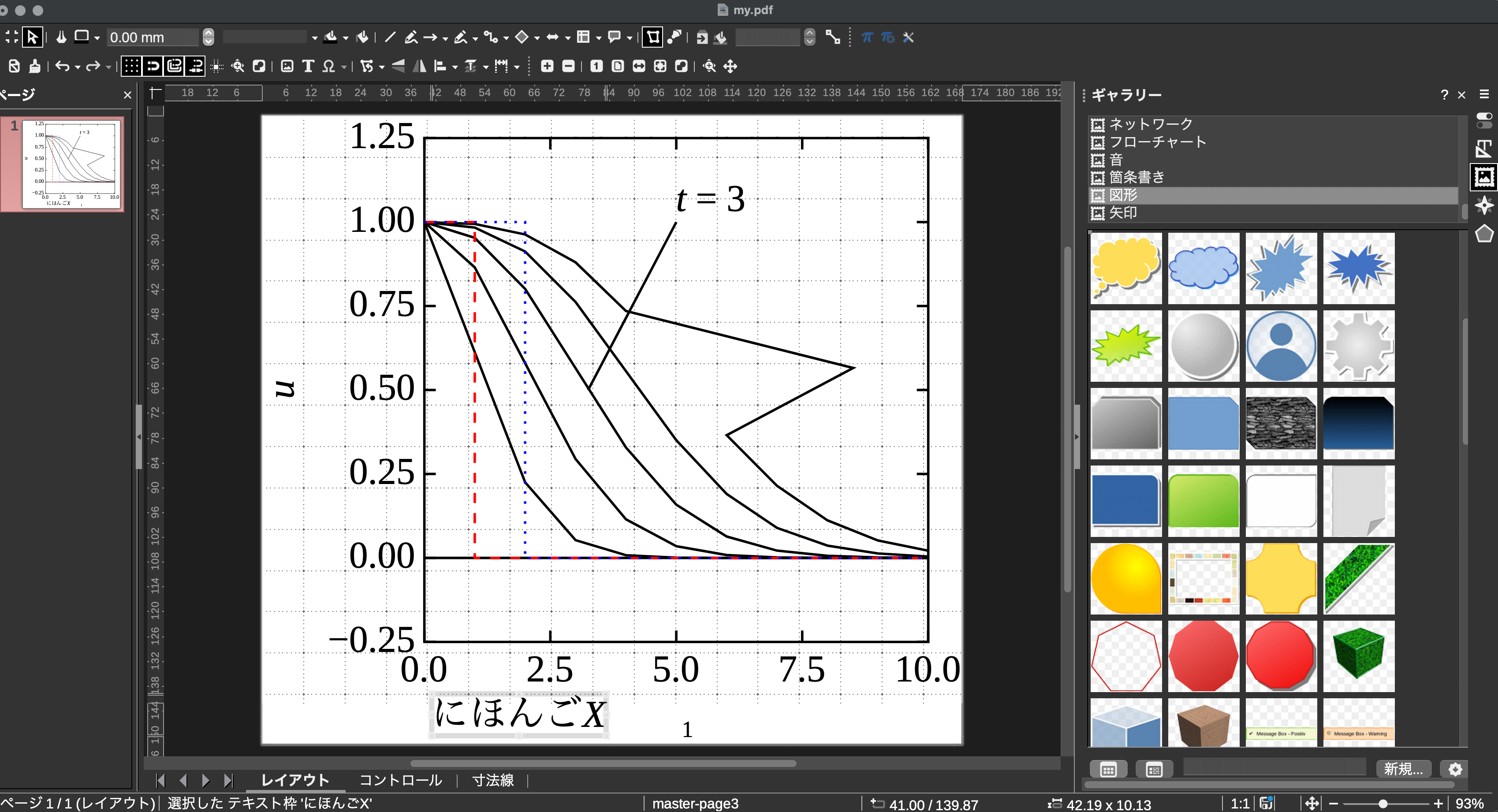 お?この人,データの改竄にもチャレンジしている・・・
お?この人,データの改竄にもチャレンジしている・・・
データ変えちゃダメだよ〜♪
陰的差分法
陽的差分法では, CFL条件によって, \(\Delta t\)を大きく選ぶことができません. 多くの問題では, 長時間経過して定常解すなわち\[\frac{\partial}{\partial t}=0\]となる状態が速く知りたいので, 困ります. そこで,
- 空間微分を, 解くべき時刻で評価する
ことを考えてみましょう. この場合, 解くべき時刻の関数値\(u_N\)に対する連立方程式が得られます(下図). 差分方程式の解が陽的に与えられず, 連立方程式の解として与えられるので, 陰的差分法(implicit scheme)と呼びます.
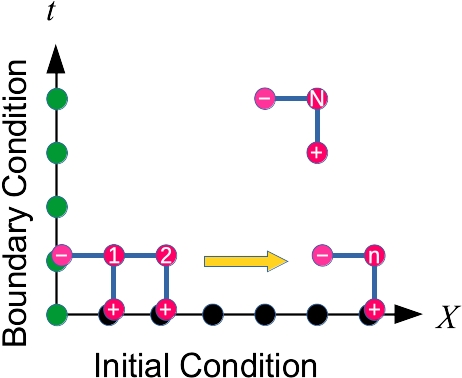
しかしこの場合,連立方程式といっても, 壁面から順番に解けば, 解が定まっていく特例になっているので, 簡単に試すことができるでしょう.
試してみよう
void Step_implicitと書いたら, AIモンキーが書きましたが,間違ってたので直させました. ううん,結構AI嘘つきますね・・・2030年くらいまでは用心して使いましょう.
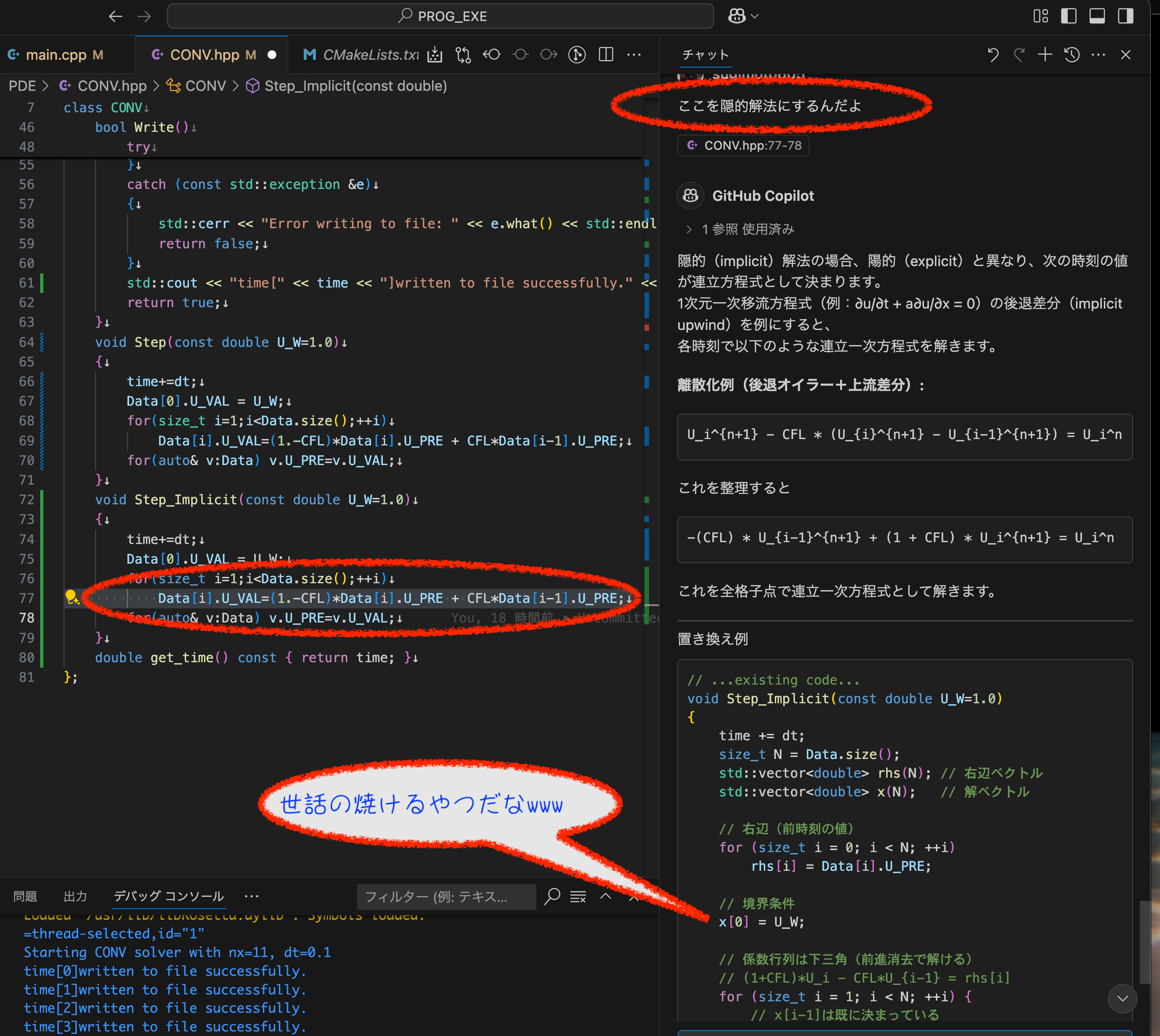
void Step_Implicit(const double U_W=1.0)
{
time+=dt;
Data[0].U_VAL = U_W;
for(size_t i=1;i<Data.size();++i) Data[i].U_VAL = (Data[i].U_PRE+CFL*Data[i-1].U_VAL)/(1.+CFL);
for(auto& v:Data) v.U_PRE=v.U_VAL;
}mainの方は
// main.cpp
#include <iostream>
#include "CONV.hpp"
int main()
{
size_t nx=10; // 空間分割数
double dt=0.1; // 時間刻み幅
size_t ntmax=50; // 最大時間ステップ数
size_t ntsave=10; // データ保存間隔
CONV mySolver(nx,dt);
mySolver.Write("Data/test03/PDE_02.dat"); // 初期状態の保存
for(size_t nt=0;nt<ntmax;nt++)
{
// mySolver.Step(); // エクスプリシットでの時間ステップ
mySolver.Step_Implicit(); // インプリシットでの時間ステップ
if ((nt+1) % ntsave == 0) mySolver.Write();
}
return 0;
}結果を比較してみると: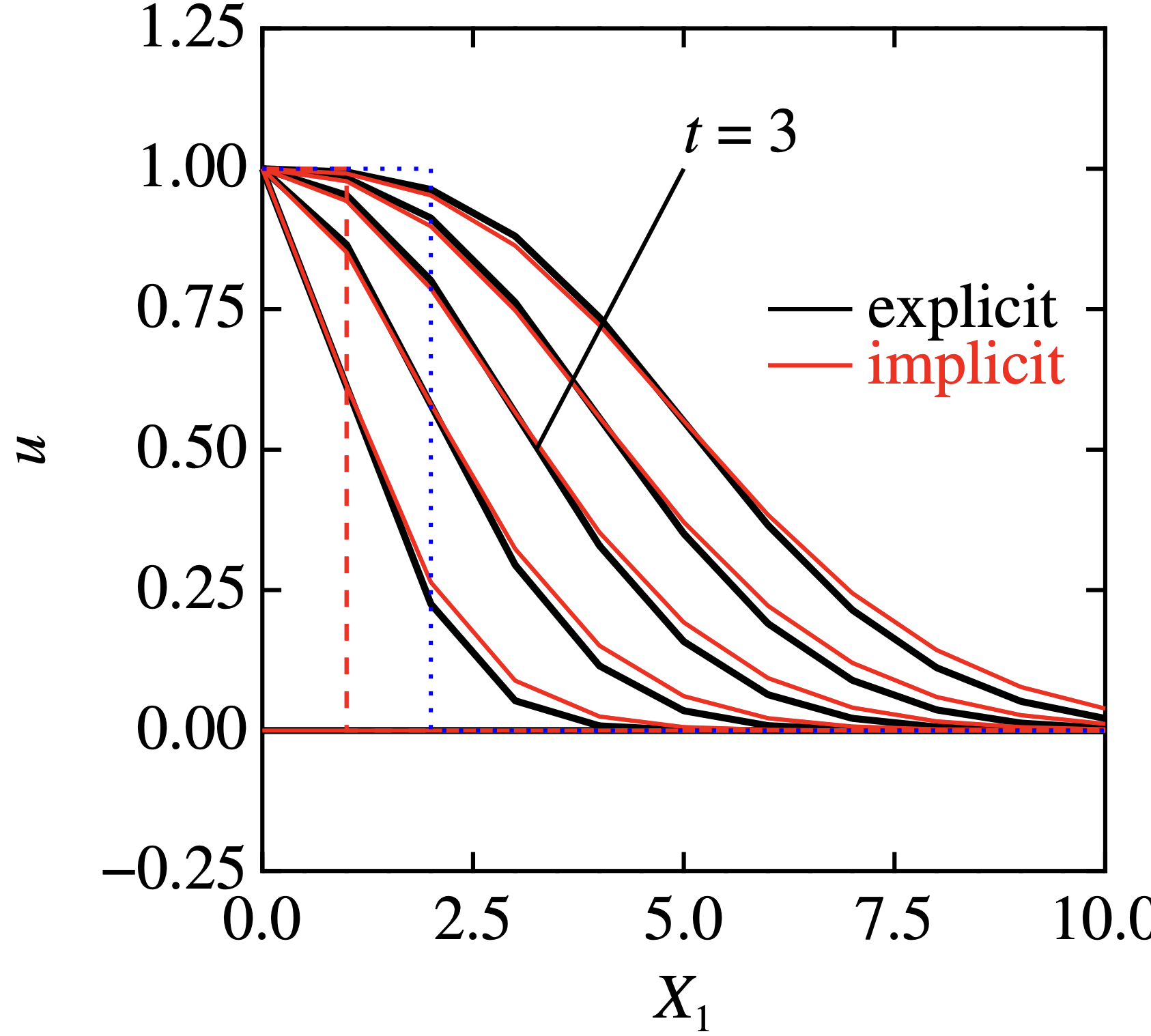 やっぱさ,なんか,インプリシットって,ダレるんだよな
やっぱさ,なんか,インプリシットって,ダレるんだよな
#!/bin/bash # PDE1.sh: 偏微分方程式I . draw.sh . standards.sh COLOR=1 X_AXIS='\fIX\sb\fR1\eb' X_RANGE='0 10 2.5' Y_AXIS='\fIu' Y_RANGE='-0.25 1.25 0.25' LINE=( Solid:Black:0.005 Solid:Red:0.003 ) SYMBOL=( Omit ) cat > $TMP/legend.dat <<@ #analytical solution t=1 #m=Dash:Red,S=Omit ←PlotUtils流力研PatchLevel9では,凡例で線の太さが変えられない 0 1 1 1 1 0 10 0
#analytical solution t=2 #m=Dot:Blue,S=Omit 0 1 2 1 2 0 10 0
#m=Solid:Black,S=Omit 3.25 0.5 5.0 1.0 lb:\fIt\fR = 3
#m=Solid:Red,S=Omit 6 0.65 7 0.65 l: implicit
#m=Solid:Black,S=Omit 6 0.75 7 0.75 l: explicit @ LEGEND=$TMP/legend.dat draw my.pdf PDE_01.dat PDE_02.dat
うえは draw.sh でグラフを描いた例です.こんな簡単な図の修正に300秒以上必要なソフトは不良品ですので,消費者センターに通報しましょう
- 実際に\(c>0\)の場合についてプログラムを作成し, \(\Delta t\)が大きくても時間発展を求められることを確かめてください.
- \(c<0\)の場合は, 差分スキームはどのようになるでしょうか?
- 差分スキームをよくみると, 内挿になっています. どの点とどの点を内挿したことになっていますか? 特性方向を用いて述べてください.
高精度差分
ここまでは, 2点のデータ\(u_{i}\), \(u_{i-1}\) を用いて最低精度の差分式を用いていました. きっと,厳密解よりもダレダレのクソデータができてしまったのは,そのせいでしょう(←嘘ですよ)
もっと点数をたくさん選べば, 精度の高い差分方程式が得られます.
例えば\(u_{i}\), \(u_{i-1}\), \(u_{i-2}\)の3点を用いる場合, \[\frac{\partial u}{\partial x}=\alpha u_{i} + \beta u_{i-1} +\gamma u_{i-2}\]となるように\(\alpha, \beta, \gamma\)を選べば良い. 具体的には, \(x_i\)周りにTaylor展開して\[u_{i}=u_{i}\], \[u_{i-1}=u_{i}-\frac{\partial u}{\partial x}(x_i)\Delta x+\frac{1}{2}\frac{\partial^2 u}{\partial x^2}(x_i)\Delta x^2+\cdots\] \[u_{i-2}=u_{i}-\frac{\partial u}{\partial x}(x_i)2\Delta x+\frac{1}{2}\frac{\partial^2 u}{\partial x^2}(x_i)4\Delta x^2+\cdots\]となるので, \(\alpha, \beta, \gamma\)を選べば \[\frac{\partial u}{\partial x}=\alpha u_{i} + \beta u_{i-1} +\gamma u_{i-2}+O(\Delta x^3)\]となるように選ぶことができます.
- 高精度の差分を用いて, 方程式を解いてみなさい.
- CFL条件は, どのように変わるか? \(\Delta t \)や\(\Delta x\)を変えて試してみてください.
時間方向に高精度の差分を用いると, 前時間ステップの分布をU_OLDにコピーしてから, 新時刻のU_VALを計算するだけでは不十分です. 前前時間ステップの分布をU_SUPEROLDにコピーしてから, 前時間ステップの分布をU_OLDにコピーしてから, 新時刻のU_VALを計算する必要があります.
で,これを初心者がやると, U_UltraPre, U_SuperPre, U_HyperPre,... とか作り出して,どの順に並んでるのかわからなくなって
U_Pre=U_SuperPre; U_HyperPre=U_Pre; U_UltraPre=U_SuperPre;
とか書き出して・・・全部同じ値になったりするんですよ.
だいたい,データが大きくなると,このようなコピーにも時間がかかるようになります.これを避けるために工夫しても良いでしょう.簡単なのは「剰余」すなわちNを3で割った余り,を考えることです.任意のNに対して,余りは0→1→2 の3通りが順番に来ますので, U[N]の代わりに,U[N%3]を使えば良いのです.まあしかし,「毎回U[N]の代わりに,U[N%3]を書く」のは通常の人類には不可能です.100回書いたら, 僕やったら10回以上はU[N]と書いたり, U[N-3]を書こうとしてU[N%3-3]を書いてしまいます(U[N%3-3]では全然ダメですよね!N%3-3の値は-3, -2, -1の3通りですからね).
std::vectorの代用pvectorを作る
普通のstd::vector<T> U(100) であれば, U[0],...U[99]はOKで, U[100]はアウトです.ですが,pVector<T> U(100)は, U[100]にアクセスすると,なぜかU[0]が返ってくる, U[301]はU[1]が返ってくる,という周期性配列です.これを実現しましょう.これがあれば, pVector<double> U(3) を定義しておけば,
U[0]=U[3]=U[6]=... U[1]=U[4]=U[7]=... U[2]=U[5]=U[7]=...
となっているので,U[nt] とか U[nt-1] と書けるわけです.
こういうのは機能拡張ですので, 本当は「継承」機能を使うべきなのですが,問題があって
- std (Standard Library)は,髭面の自称神とかの仲間が作ったものなので,そのコードに触れることは禁則事項である
- 古よりのしきたりに反して中身を覗いた場合,あなたのプログラムに,大きな災いが起こると伝えられておる
- どうせ読んでもわからない.そんなことができるのなら数理解析研究所の難しい数学の本も全部わかるはずだ
なので,もっとお手軽に
- メンバー変数のstd::vector にアクセスできれば良い
と考えましょう.計算速度は落ちますが,プログラム作成速度の向上が見込めます.こういう,「隠れメンバーの使い方を指定して機能だけ使う」プログラムを, 手で持てないチキンやサーモンをトルティーヤで包んで食べやすくする感じで「ラップ」とか「ラッパー」と言います.
概要を作成
pvector.hppを作成すると, AIモンキーが「名称から察するに,これっすか」と書いてくれました.
// pvector: Periodic vector array
// author: VSCode-copilot, not you
#pragma once
#include <iostream>
#include <vector>
#include <cmath>
class pvector
{
std::vector<double> data;
public:
pvector(size_t size = 0) : data(size) {}
double &operator[](size_t index) {return data[index];}
const double &operator[](size_t index) const {return data[index];}
size_t size() const {return data.size();}
void resize(size_t newSize){data.resize(newSize);}
};うまくできていますが,ここいら辺がわからないので解説しましょう.ああ,この辺はさすがAI, 気が利いてますね!
オペレータの定義
std::vector<double> U であれば, U[23]で, 24番目の数値にアクセスできます.また, std::vector<double> V との計算U+Vとかも可能です. このような演算子(オペレータ)を, C++ではオペレータと呼びます.そのままやんけ.
クラスに対する可能な主要なオペレータは:
- 添字オペレータ [N] 整数Nを一つ与えると, 何かが得られる. ま,普通は?N番目に対応する要素が得られる
- 関数オペレータ (引数,...) 引数を与えると,何かが得られる.
- 四則演算 +-*/ A+BとかA/Bとかを行うと,何かが得られる
- 代入演算 A=B を行うと,何か奇妙なことが起こる.通常, Bの複製がAに代入される
- 比較演算 <><=とか A>=B とかやると,通常 true か false が返ってくる
- 出力演算 << 画面出力も演算なんですね.
- 他にもいっぱいあるけど面倒
で,猿が作ったサンプルでは, [N]が2通り定義されてますね.double& を返すやつは,意図が簡単.参照&になっているので,
std::cout << U[3] << std::endl; //U[3]の値を読み出して画面に出す U[3]=3.5; //U[3]の値を3.5に変更
が可能です.&を付けない場合, U[3]は値のコピーを返しますので,U[3]=3.5 ではコピーの値を書き換えた後,コピーを破棄します(要するに何も起こらない).さて,double& オペレータだけだと, この辺のクソ事情に引っかかるケースがあるので, const double& バージョンも念のために作られている.C++コンパイラは,どちらか適切なものを呼び出します.まあ,計算が遅くてよろしいのであれば,こんなこと気にする必要はないです.計算が遅い方が,「僕の仕事はとても大変」感が出て,外部からの評価が上がるケースもあります.ま,その手を使うかどうかは個人の倫理観で自由です.
出力演算?!?
出力演算オペレータは, デバッグとかで超絶便利です.あんたのクラスの定義の後ろに,こげな定義を追加するだけ:
class MyClass
{
....
};
// define global operator
inline std::ostream& operator<<(std::ostream& os, const MyClass& m)
{
os << "MyFormat of MyClass is " << m.n << " Tempereature " << m.T;
return os;
}
std::ostream ってのは, 下の継承で学ぶ基底クラスで, まあなんというか「どこかに出力する人たち」一般を指すクラスです. 基底クラスで可能なことは,それを「継承」した人たち(ファイルに出力,画面に出力・・・)全てで有効になります.この&は,前節登場の参照です.inlineってのは, まあ簡単な関数なので,実行ファイルを作るときに毎回人間がこれを描いたかのように扱え,その方が早いから.という意味です.constと書いてあるのは・・・AIに書いてもらったんで,まあ付けたほうがいいんですよ. で,肝心なのがこの辺で,ここはMyClassの内容に応じて,「画面に書くんだったら毎回こうやって欲しい」を書きます.
これで,どんな複雑怪奇なクラスでも,画面出力が
MyClass myObj,
...
std::cout << myObj << std::endl;
で済みます.毎回ガタガタ書かなくて良いので,楽ちんです.すると, 「いやそれなら,出来合いのEigen::Vector2dとかでも,俺の好きなふうに書いて欲しいんだが?」と思いますよね,あなたも.それは,まあ共通で入っているhppファイルのどれか適当なところに,こう書いてしまいましょう:
//constants.hpp
...
inline std::ostream &operator<<(std::ostream &os, const Eigen::Vector3d &v)
{
os << v[0] << "," << v[1] << "," << v[2];
return os;
}
これで, std::cout << myEigenVector << std::endl で, 0.232323,0.2223323,-04232323 というふうに出力してくれますよ
Range対応
このままだと, for(auto& v:Data)が使えないので追加しましょう:
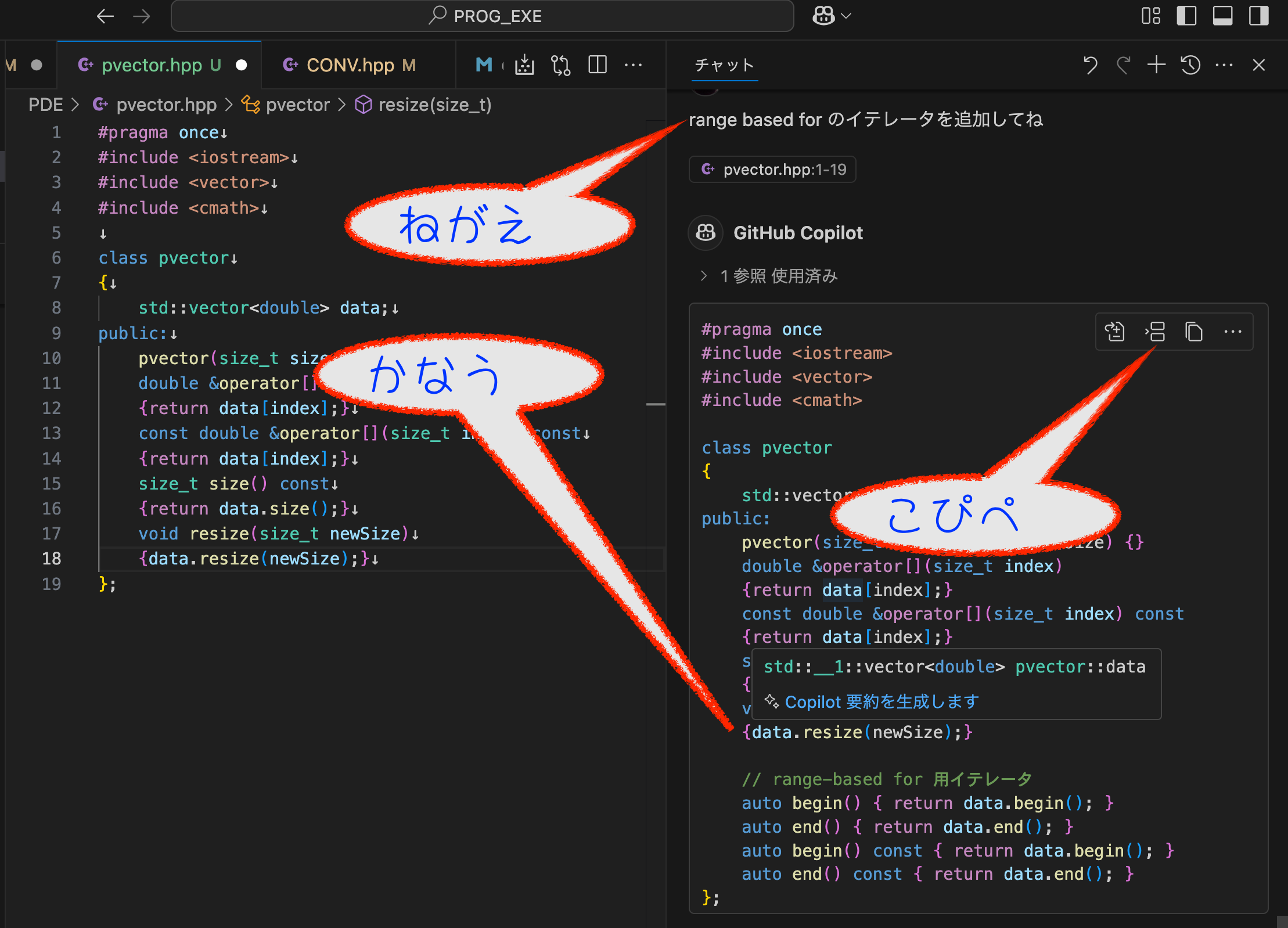
関数値の戻り値が, 型推論 auto という極楽技も覚えましょうね!人間がプログラム書くとバグるので!変数の型名なんて, autoでダメなら考えたら良いんですよ.
周期の実装
では, 周期を実装しましょう!
詳細
できたつもり(バグっている)
// pvector.hpp
#pragma once
#include <iostream>
#include <vector>
#include <cmath>
class pvector
{
std::vector<double> data;
public:
pvector(size_t size = 0) : data(size) {}
auto &operator[](size_t index)
{return data[index % data.size()];}
const auto &operator[](size_t index) const
{return data[index % data.size()];}
auto size() const
{return data.size();}
void resize(size_t newSize)
{data.resize(newSize);}
// range-based for 用イテレータ
auto begin() { return data.begin(); }
auto end() { return data.end(); }
auto begin() const { return data.begin(); }
auto end() const { return data.end(); }
};お客様に届ける前に,動作点検しましょうね.
// main.cpp #include <iostream> ... #define _TEST #ifndef _TEST ... #else std::cout << "This is a test build. No PDE solver executed." << std::endl; pvector Data(7); std::cout << "SIZE: " << Data.size() << std::endl; for (size_t n=0;auto &v : Data) v=n++; for(int i=-10;i<10;i++) std::cout << "Data[" << i << "] = " << Data[i] << std::endl; #endif ...
ここは範囲forで, 数えることができるという小技です.まあどうでも良いか.いや, ここで, n++ と ++n は異なる.というのもポイントですかね.
-
前者はnをvに代入してから, nを1増やす.Data[0]=0, Data[1]=1, ... になる
-
後者は, nを1増やしてから, vに代入する.Data[0]=1. Data[2]=2.... になる
問題は,ここで,Data[-3]だとどうなるんだ?ということです.クラスの方では引数がsize_tですので,負の数値を受け取れません.ここは正しくはintにしとかないと,ダメです.それで良いのかと思って実行すると,あらあら不思議,
This is a test build. No PDE solver executed. SIZE: 7 ... Data[-3] = 6 ←ありゃ?ここは,4 Data[-2] = 0 ←ありゃ?ここは,5 Data[-1] = 1 ←ありゃ?ここは,6 Data[0] = 0 Data[1] = 1 ...
C++のN%Mの実装は, Mが整数の時と非負整数の時で異なり,ちょっと訳がわからないです.
int n1 = 7;
unsigned int n2 = 7;
size_t n3= 7; // index=-1 -2 -3 -4 ... -6 -7
int val1 = index % n1; // val1 =-1 -2 -3 -4 ... -6 0 これは sign(N)*abs(N)%M
int val2 = index % n2; // val2 = 3 2 1 0 5 3 おそらく -7 を32bit非負整数に変換してから計算
int val3 = index % n3; // val3 = 1 0 6 5 3 2 おそらく -7 を64bit非負整数に変換してから計算こんなものと格闘している暇はないので,AIモンキーに直してもらいました. あれ?僕が使ってるのより式が簡単だな
// pvector.hpp
#pragma once
#include <iostream>
#include <vector>
#include <cmath>
class pvector
{
std::vector<double> data;
auto pindex(int index) // インデックスを正の値に変換するヘルパー関数
const {
int n = data.size(); // size()は非負整数size_tなのでintに変更
return ((index % n) + n) % n;
}
public:
pvector(size_t size = 0) : data(size) {}
auto &operator[](int index)
{return data[pindex(index)];}
const auto &operator[](int index) const
{return data[pindex(index)];}
auto size() const
{return data.size();}
void resize(size_t newSize)
{data.resize(newSize);}
auto begin() { return data.begin(); }
auto end() { return data.end(); }
auto begin() const { return data.begin(); }
auto end() const { return data.end(); }
auto front() { return data.front(); }
auto back() { return data.back(); }
};この辺は,後の都合で入れてあります.これで正常:
This is a test build. No PDE solver executed. SIZE: 7 Data[-10] = 4 Data[-9] = 5 Data[-8] = 6 Data[-7] = 0 Data[-6] = 1 Data[-5] = 2 Data[-4] = 3 Data[-3] = 4 Data[-2] = 5 Data[-1] = 6 Data[0] = 0 Data[1] = 1 Data[2] = 2 Data[3] = 3 Data[4] = 4 Data[5] = 5 Data[6] = 6 Data[7] = 0 Data[8] = 1 Data[9] = 2
♪
さてこれでpvector U(3)とかで周期性配列が作れます.ですが,std::vector<double> U(3) とは,この辺が違いますね?で, ここには僕のクラスとか,任意のものが入れられて, それはそれで便利でした.これはなんなのでしょう?
std::vector<T>の代用pVector<T>を作る
pvectorは,倍精度数doubleの配列限定でした.もしかすると, 整数intの周期性配列が必要になるかもしれません.そのときには,どうしましょうか.
- ぺろろーんと,pvector.hpp を new_pvector.hpp にコピーする
- もっといろいろひつようなら,new_super_pvector.hpp とか, newnew_super_ultra.hpp, new_super_new_ultra.hpp を作成
- double と書いてあったところを, int とかに直す
これでいいのです.ところが,これだと実装数が増える.修士課程を卒業するとき,こんなノリで「かすかに違うプログラムが45種類ある」になってました.バグが見つかるたびに45種類直すのですが,ときどき,いくつか訂正し忘れて,計算をやり直してました.
人間が,コピペして訂正,という作業をするべきではないです.機械にやらせましょう. それをクラス・テンプレートと呼びます.
クラス・テンプレートの書き方
AIモンキーに「これ,テンプレートにして」と頼めば一発です:
一発っすね
下がtemplate です.template はTを与えるとクラスになるものであって,Tが未定の場合,クラスではないです.
#pragma once #include <iostream> #include <vector> #include <cmath> template<typename T> class pvector { std::vector<T> data; auto pindex(int index) // インデックスを正の値に変換するヘルパー関数 const { int n = data.size(); return ((index % n) + n) % n; } public: pvector(size_t size = 0) : data(size) {} auto &operator[](int index) {return data[pindex(index)];} const auto &operator[](int index) const {return data[pindex(index)];} auto size() const {return data.size();} void resize(size_t newSize) {data.resize(newSize);} auto begin() { return data.begin(); } auto end() { return data.end(); } auto begin() const { return data.begin(); } auto end() const { return data.end(); } };
変更されたのは黄色のところだけです.Tのところがdoubleならdoubleの配列が,myClassならmyClassの配列ができます.もちろん,不用意に T と書いてある型名は,全て検索置換されてしまうので,気をつけましょうね.
これで pvector<double> myV でdoubleの配列が, pvector<long> myLongInt でlong int の配列が, pvector<Fuck> fWords でFuckクラスの周期性配列が作成できます.
Advection EquationそのII
せっかくpvectorクラスを作成したので, 周期問題\[\dfrac{\partial u}{\partial t}+c\dfrac{\partial u}{\partial x}=0,\qquad u(t,0)=u(t,1),\qquad \lim_{t\to 0} u(t,x)=g(x)\]を解いてみましょう.
Explicit解法
では,書いていきましょう.
メンバー変数・ コンストラクタおよびその 試験結果について
まずは概要ですよね.
// pCONV.hpp Solve advection equation using explicit method. Periodic problem
#pragma once
#include <iostream>
#include <filesystem>
#include <cmath>
#include <vector>
#include <fstream>
#include "pvector.hpp"
class pCONV
{
double dt, CFL;
double time;
int nt = 0; // 時間ステップのカウンタ
class Point
{
public:
Point* pre = nullptr; // ポインタを追加して前のポイントへのリンクを作成
double X;
pvector<double> U; // U_n
Point() : U(3) {} // デフォルトコンストラクタでサイズ3のpvectorを初期化
auto &operator[](int index) { return U[index]; }
const auto &operator[](int index) const { return U[index]; }
};
pvector<Point> Data;
std::ofstream ofs;
public:
pCONV(const size_t &nx, const double &dt, const std::function<double(double)> &U0 = [](double x)
{ return 0.; }) : dt(dt)
{
double xmax = 1.0;
time = 0.0; // 初期時間
double dx = xmax / nx; // 空間刻み幅の計算
CFL = dt / dx; // CFL条件の計算
Data.resize(nx); // 空間分割数に基づいて初期化
for (size_t i = 0; auto &P : Data)
{
P.pre = &Data[i - 1];
P[nt] = P[nt - 1] = P[nt - 2] = U0(P.X = i * dx); // 初期条件の適用
i++;
}
std::cout << "Starting pCONV solver with nx=" << Data.size() << ", dt=" << dt << std::endl;
for(auto& P:Data)
{
std::cout << std::setprecision(5) << std::fixed << std::showpos
<< P.X << " : " << P[nt] << " " << (*P.pre)[nt] << std::endl;
}
}ここは新顔です.前回, Pointに番号をつけたのですが, あまり使い道がなかったので,今回は左側のPointへのポインターを装備してみました.Pointクラスは,ここではまだ定義中であるのですが,自分自身へのポインタは使えるのです.
そもそも,ポインターは「住所」ですので,「あー住所か.なら全角文字30文字の入力欄作っとけば,まあ,はいるやろ」という程度しか考える必要がないので,
class B; class Point { ... B* ptrB; ...
と書いても問題はない.Bは少なくともクラスであることは明らかで,ここには住所欄を作れば良いだけ.「Bに含まれるこの関数」「Bに含まれるこの変数」とかを述べるのでなければ,OKです.こういうのを, 前方宣言と言います.
で,prevフィールドの使い方ですが,ここで,左隣の点を指差せ,と指定していますね!
Pointクラスにもオペレータを装備しているので, Data[nx]が, nx番目の格子点のデータで, 時刻ntのUの値は, Data[nx][nt] でアクセスできることになりました.で,この辺はテストです.
for(auto& P:Data)で, PはPointインスタンスになっている. P.preは左隣のPointを指さしているので*でインスタンスに戻して, それも値を画面出力.このへんは, 桁数を固定とか, 符号出しとけ,という指示で,
Starting pCONV solver with nx=10, dt=0.02 +0.00000 : +0.00000 -0.07016 +0.10000 : +0.07016 +0.00000 +0.20000 : +0.77809 +0.07016 +0.30000 : +0.77809 +0.77809 +0.40000 : +0.07016 +0.77809 +0.50000 : +0.00000 +0.07016 +0.60000 : -0.07016 +0.00000 +0.70000 : -0.77809 -0.07016 +0.80000 : -0.77809 -0.77809 +0.90000 : -0.07016 -0.77809
ほれ.Xの値 : 自分の値と,左隣の値が出力されてますね!これは, main()で
pCONV mySolver(nx,dt,[](double x) { return std::pow(std::sin(2.0 * M_PI * x),5); }); // 初期条件として正弦波を設定と指定したケースです.初期値が\(\sin^5(2\pi x)\)となっています.
スキームについて
では時間発展を記述しましょう. それ以外のWriteとかは,流用で.前回作成した1次精度・妖怪法スキームは
// pCONV.hpp
...
void StepLQ() // 1次精度, explicit method
{
time = (++nt) * dt;
for(auto& P:Data) P[nt]=(1.-CFL)*P[nt-1]+ CFL*(*P.pre)[nt-1];
}
こうなっちゃいますね. Pは各格子点データ, P[nt]は(ここで1増やしているので)次時刻の値で,これは左の格子点のデータです. では, 空間微分を高次精度にしてみましょう:
void StepHQ()
{
time = (++nt) * dt;
for (auto &P : Data)
{
auto& Pn1=*P.pre; //左隣
auto& Pn2=*Pn1.pre; //左左隣
P[nt] = (1.-1.5*CFL)*P[nt - 1] +2.*CFL*Pn1[nt-1]-0.5*CFL* Pn2[nt - 1];
}
}結果はこんな感じで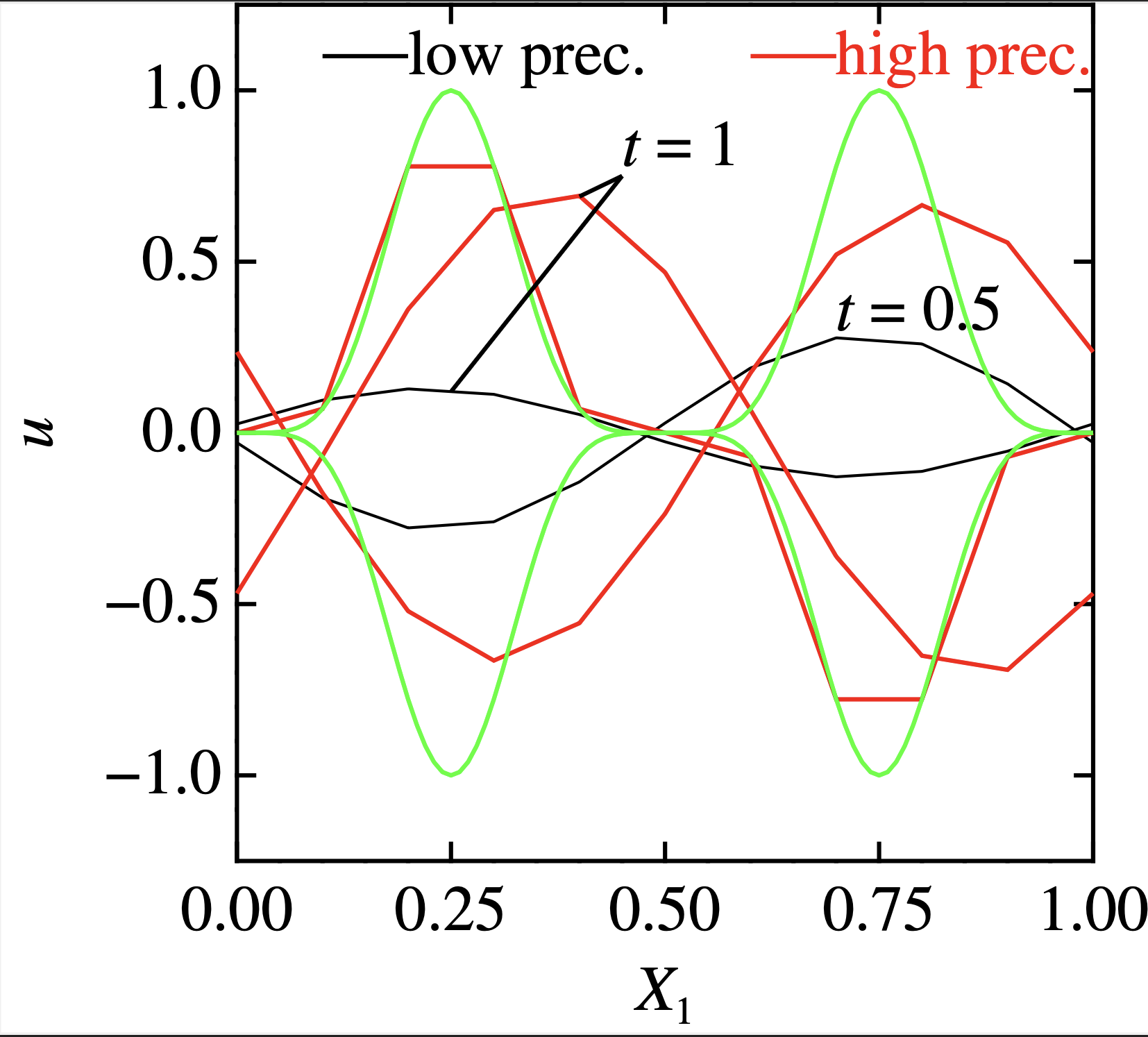 緑が厳密解です.格子点数10, CFL=0.2
緑が厳密解です.格子点数10, CFL=0.2
低次精度では1周する間に波が減衰してしまっている.時間1次-空間2次のは,波の減衰は少ないが,波の速度が,あまり正確ではないですね・・・
- 空間格子数が10点では,流石に難しいな.もう少し増やしてみよう.
- 他のスキームも試してみたい・・・となると,次の継承を覚えた方が良い.
- なお,この図を描くdrawスクリプトは
#!/bin/bash
# PDEh.sh: 偏微分方程式I: 周期解
. draw.sh
. standards.sh
COLOR=1
X_AXIS='\fIX\sb\fR1\eb'
X_RANGE='0 1 0.25'
Y_AXIS='\fIu'
Y_RANGE='-1.25 1.25 0.5'
LINE=( Solid:Black:0.002 Solid:Red:0.003 Solid:Green:0.003 )
SYMBOL=( Omit )
#解析解のデータが,欲しい
seq 0 1|\
gawk '
BEGIN{pi=4*atan2(1,1);}
{
time=$1*0.5;
printf("#time= %f\n",time);
for(i=0;i<101;i++)
{
x=i/100;y=sin(2*pi*(x+time))^5;printf("%f %f\n",x,y);
}
printf("\n");
}
END{printf("\n");}' > $TMP/sol
#凡例
cat > $TMP/legend.dat <<@
#m=Solid:Black,S=Omit
0.1 1.1
0.2 1.1 l:low prec.
#m=Solid:Red,S=Omit
0.6 1.1
0.7 1.1 l:high prec.
#m=Solid:Black,S=Omit
0.70 0.25 lb:\fIt\fR = 0.5
0.45 0.75
0.40 0.69
0.45 0.75
0.25 0.12
0.45 0.73 5lb:\fIt\fR = 1
@
LEGEND=$TMP/legend.dat
draw my.pdf PDE_LQ.dat PDE_HQ.dat $TMP/solこんな感じです.
にゃあ
継承
さて, 伝達方程式の境界値問題を解く CONV.hpp と, 周期解問題を解く pCONV.hpp を作りましたが・・・・なんか,そっくりですよね.
- 配列データ Data を使う
- ファイルを保存する Write(filename), Write()がある
- 時間を進める Step()があるが,内容は異なる
これはヒトでいえば
- 真核生物:細胞に核がある
- 新口生物:食物を導入する穴と,排泄物を出す穴は, 別の方が気持ちよい
- 脊椎動物:内骨格を有する
- 四肢動物:4つの体肢を装備
- 哺乳類:首の骨は7個で決定
- 霊長類, 狭鼻目,ヒト上科,ヒト・・・
- 哺乳類:首の骨は7個で決定
- 四肢動物:4つの体肢を装備
- 脊椎動物:内骨格を有する
- 前口動物:メシとうんこが同じ口では嫌というアイデアは共通だが前後が逆
- 脱皮動物・・・
- 新口生物:食物を導入する穴と,排泄物を出す穴は, 別の方が気持ちよい
と特殊化が進んでいって,ヒトになったのです.「4つの体肢を装備」する特徴はヒトも鳥類も同じで,毎度新たに炭素や水素から進化してるわけではない(一発の進化で30億年かかるので,生物の数だけ毎回進化してたら太陽がなくなってしまう).なので,ここいらへんの特徴を有する生物をまず作っておいて,ここいら辺が違う,と書いた方が簡単です.これを,ご先祖様の特徴を継承する,と言います.
C++は, 多重継承というのが可能で,上の例で言えば哺乳類と脱皮動物の両方を継承することができます!そうしたら,あなたも朝になったら脱皮しているかもしれませんね.というわけで,多重継承は他の言語から「キモい」という評価を受けてます.わかりにくくなるので(口と肛門が,たまに逆さまに位置する場合があるので,日常生活に多少の不自由がある),しばらくはやめときましょう.
生物Aが特殊化して生物Bに進化したとき, 生物Aを基底クラス, 生物Bを派生クラスと呼びます.
基底クラスを書いてみよう
従来の CONV.hpp とかをコピーして, 何かこう基底ファンダメンタルな感じの名前にしておきます. で,改造
// pSolver1DBase.hpp Solve some equation using some method. Periodic problem
#pragma once // この辺は同じ・・・てゆうか,基本,同じ
#include <iostream>
#include <filesystem>
#include <cmath>
#include <vector>
#include <fstream>
#include "pvector.hpp"
template <typename T>
class pSolver1DBase
{
protected:
double xmax = 1.0;
double dt, CFL;
double time;
int nt = 0; // 時間ステップのカウンタ
class Point
{
public:
Point *pre = nullptr; // ポインタを追加して前のポイントへのリンクを作成
double X;
pvector<T> U; // U_n
Point() : U(3) {} // デフォルトコンストラクタでサイズ3のpvectorを初期化
auto &operator[](int index) { return U[index]; }
const auto &operator[](int index) const { return U[index]; }
};
pvector<Point> Data;
std::ofstream ofs;
public:
pSolver1DBase(const size_t &nx, const double &dt, const std::function<double(double)> &U0) : dt(dt)
{
double C = 1.0; // 速度
time = 0.0; // 初期時間
double dx = xmax / nx; // 空間刻み幅の計算
CFL = C * dt / dx; // CFL条件の計算
Data.resize(nx); // 空間分割数に基づいて初期化
for (size_t i = 0; auto &P : Data)
{
P.pre = &Data[i - 1];
P[nt] = P[nt - 1] = P[nt - 2] = U0(P.X = i * dx); // 初期条件の適用
i++;
}
std::cout << "Booting pSolver1DBaase with nx=" << Data.size() << ", dt=" << dt << std::endl;
}
std::string what() const
{
return "pSolver1DBase: nx=" + std::to_string(Data.size()) + ", dt=" + std::to_string(dt) +
", CFL=" + std::to_string(CFL) + ", time=" + std::to_string(time);
}
bool Write(const std::string &filename)
{
if (ofs)
ofs.close(); // 既存のファイルストリームを閉じる
std::filesystem::path datafile = getenv("HOME");
datafile /= filename;
std::filesystem::create_directories(datafile.parent_path());
ofs.open(datafile);
if (!ofs)
throw std::ios_base::failure("Failed to open file: " + datafile.string());
return Write();
}
bool Write()
{
try
{
ofs << std::endl
<< "# nt= " << nt << " time= " << time << " CFL= " << CFL << std::endl;
for (auto &v : Data)
ofs << v.X << " " << v[nt] << std::endl;
ofs << Data.front().X + xmax << " " << Data.front()[nt] << std::endl; // 最初のデータを追加
}
catch (const std::exception &e)
{
std::cerr << "Error writing to file: " << e.what() << std::endl;
return false;
}
std::cout << "time[" << time << "]written to file successfully." << std::endl;
return true;
}
virtual void Step(double U_W=0.0)=0;
virtual void Initialize(void *parm=nullptr) {};
double get_time() const { return time; }
};
ほとんど元のままですが,
- クラス名は変えたよ. 起動の様子とかみたかったんで,こことかここは,名前を入れたらAIがこうしろっていう
- ここはテンプレートを学んだので,いたずら心でやってみた.
- ここはなんだ?以前は何も書いてなかったので黙ってprivate変数でした.で,private変数は本当にプライベートで,派生型からもアクセスできません.派生型からは見えるけど,外部からは見えない変数が protected 変数です.
- virtual というのをつけると, 「派生型かどうか調べてから,合致するのを使う」となります. virtualでない関数は,定義されていればそのインスタンスの宣言文に多応するクラスの関数が呼び出されます.
- で, virtrual 関数にデフォルトの関数を定義しても良い. ここでは,関数定義{.....} を,ガバッと =0 と書いています.これは
- 基底クラスをインスタンスにできない
- 派生クラスを作成する場合, =0 にしてある関数を,必ず絶対抜かりなく定義しなければならぬ.=0が残っている場合,インスタンスにできない.
- これで,定義し忘れミスを防ぐことができる.
- まあ今のところ使い道がありませんが,こういう,追加の作業が記述できる関数を用意しておくのもありですね.
派生クラスを書いてみよう
では,派生してみましょう.簡単のため,最初に作った低精度スキームを書いてみます.
// pSolverLD.hpp
#include "pSolver1DBase.hpp"
class pSolverLD : public pSolver1DBase<double>
{
public:
pSolverLD(const size_t &nx, const double &dt, const std::function<double(double)> &U0 = [](double x){ return 0.; })
: pSolver1DBase(nx, dt, U0)
{
std::cout << "Booting pSolverLD..." << std::endl;
}
void Step(double U_W = 0.0) override
{
for (auto &P : Data) P[nt+1] = P[nt] - CFL * (P[nt] - (*P.pre)[nt]);
time = (++nt) * dt;
}
};
まずここで規定クラスを読み込みます.で,派生クラスの定義では,この辺に public と書いてから,基底クラス名を入れます(今回はたまたま基底クラスがテンプレートなのでdoubleで指定).で,コンストラクトする際に,基底クラスのコンストラクタを呼び出しましょう!で,基底クラスで=0になっていた関数を,全て定義していきます!このoverride ってのは, 最近は書いた方が絶対良い(省いてもエラーではない)らしいです.
これで,「基本的には基底クラスなんじゃけど」「基底クラスでやること全部やってから」「特殊なのはここね♪」と,書けました.
main()
main()では,まあ普通な感じで使えばよろしい . 読み込むのは派生クラスの定義だけでいいよ:
// main.cpp
#include <iostream>
#include "pSolverLD.hpp"
int main()
{
size_t nx=10; // 空間分割数
double dt=0.02; // 時間刻み幅
size_t ntmax=50; // 最大時間ステップ数
size_t ntsave=25; // データ保存間隔
pSolverLD mySolver(nx, dt, [](double x)
{ return std::pow(std::sin(2.0 * M_PI * x), 5); }); // 初期条件として正弦波を設定
mySolver.Write("Data/test03/PSOLVER_LD.dat"); // 初期状態の保存
for(size_t nt=0;nt<ntmax;nt++)
{
mySolver.Step(); // 時間ステップを実行
if ((nt+1) % ntsave == 0) mySolver.Write();
}
return 0;
}
実行してみると,
Booting pSolver1DBaase with nx=10, dt=0.02 ←基底コンストラクタが走って
Booting pSolverLD... ←派生コンストラクタが走って
time[0]written to file successfully. ←Write()は規定のやつ.
time[0.5]written to file successfully. メッセージは出てないけど, Step()は派生のやつが動く
time[1]written to file successfully.
これで,別のスキーム試したい時には,派生クラスを一つ作って,違う部分だけを書く.ができますね.
遊べ!とりあえず遊べ!遊ばない者に未来はない
遊べるようになったので,計算スキーム競争をしてみるのもよかろう. どのように遊んだらいいのか,を先生に聞くような愚か者は,この大学には存在しないはずだ.
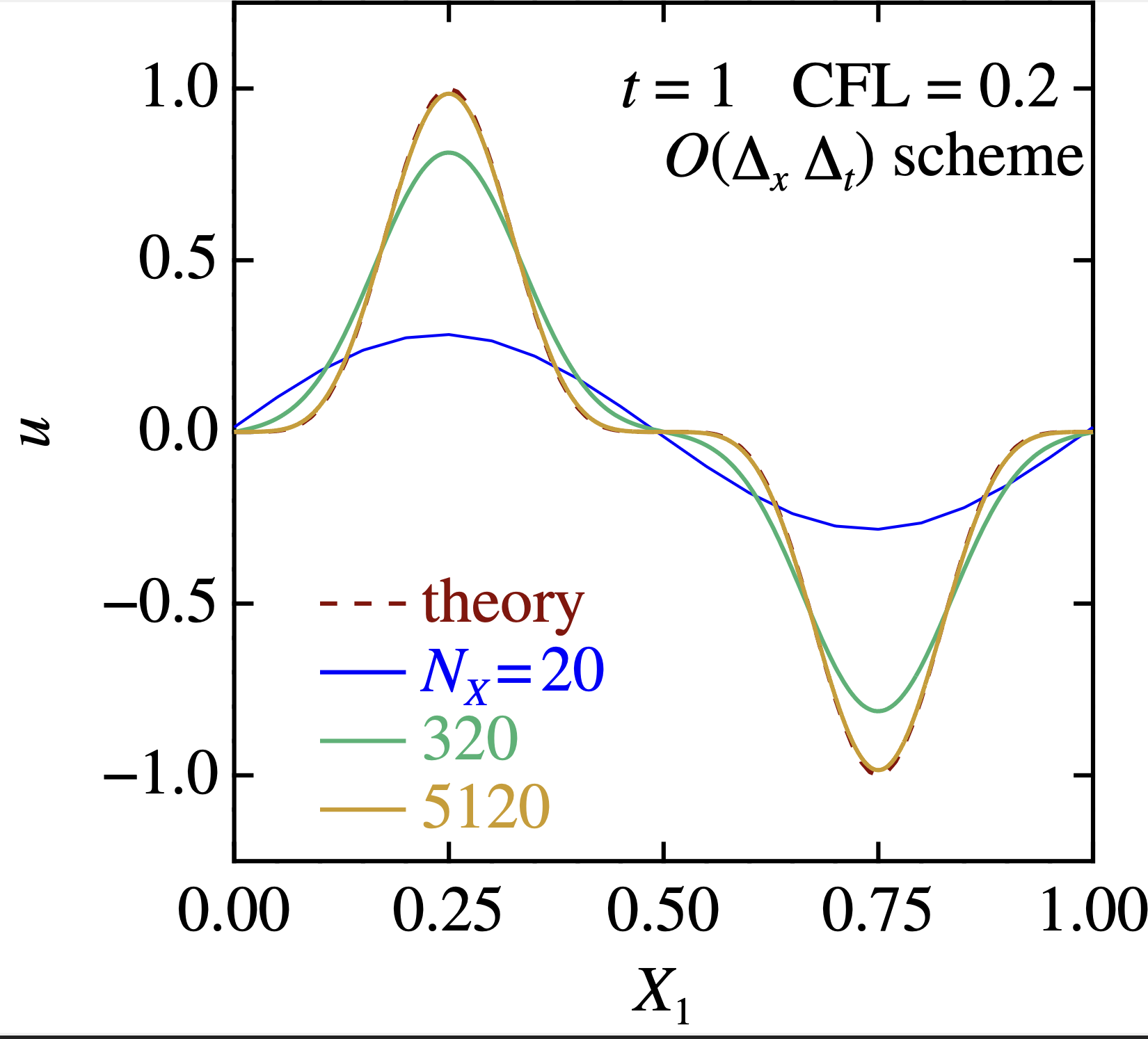
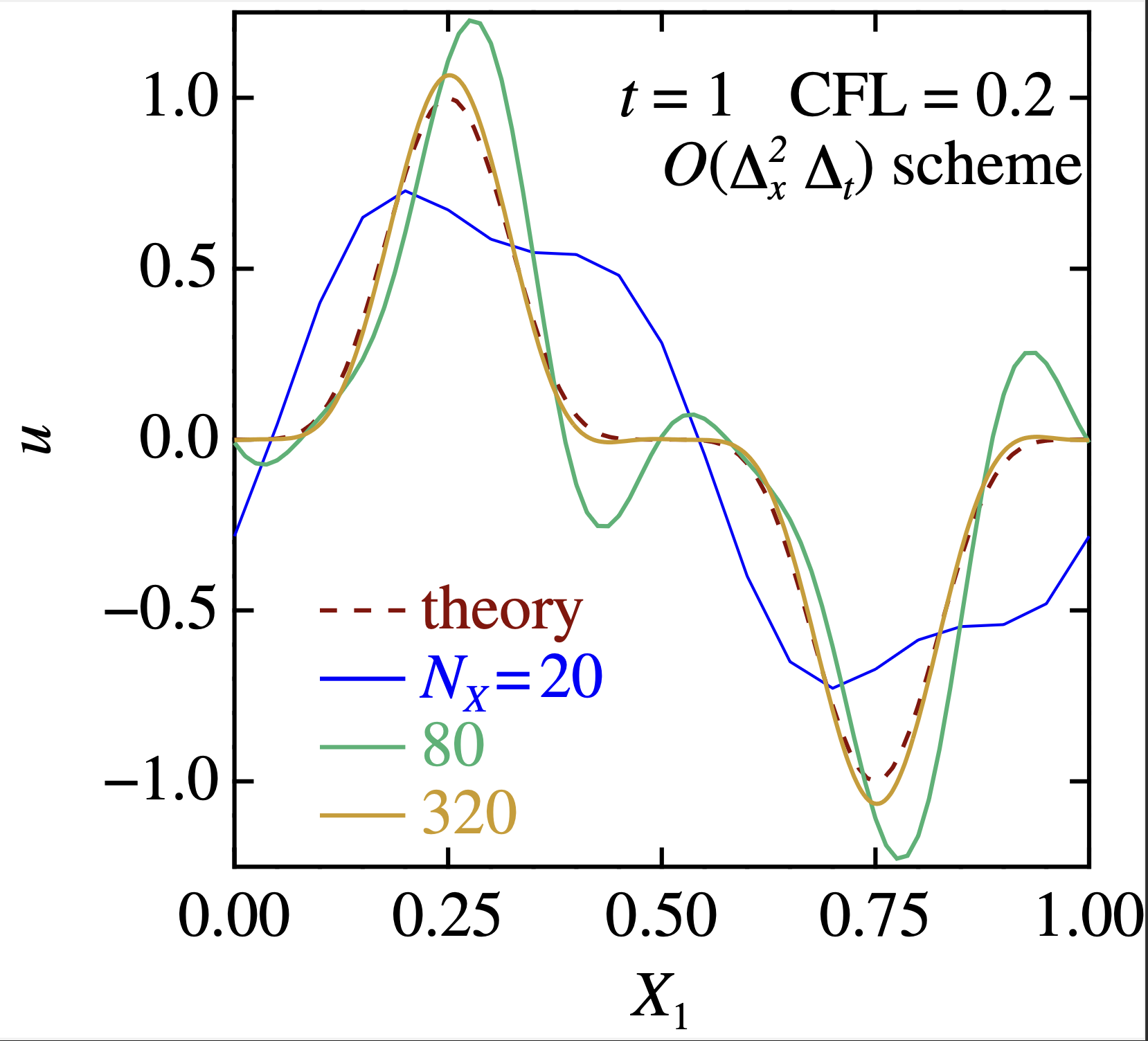
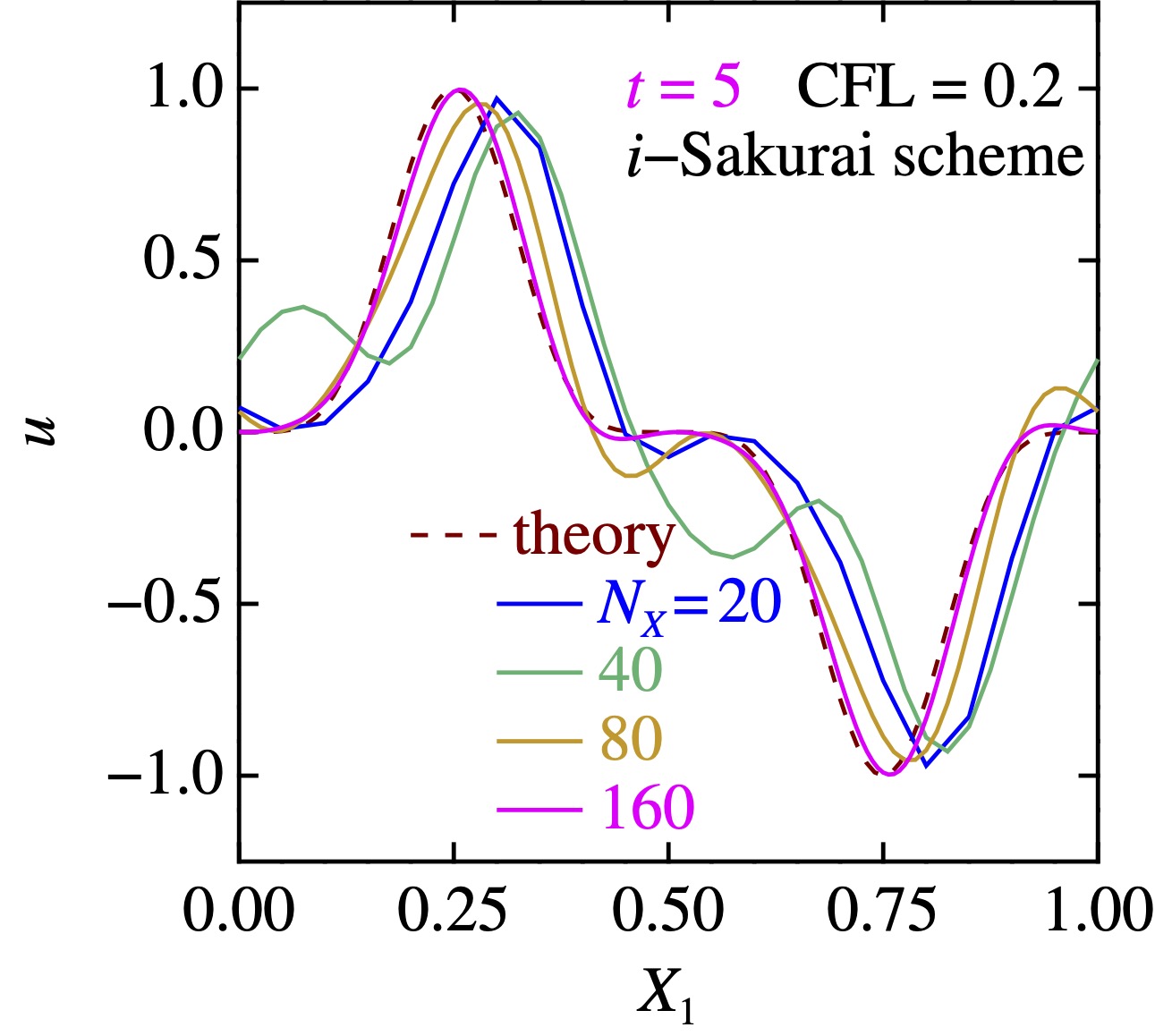
一番左は, 低次精度スキーム. 解は穏やかだが, 基本はダレダレで,まともな答えを出すには力押し(5120格子)が必要である!金はあるが暇はないヒト向け.
真ん中は,高次精度スキーム. 訳のわからない挙動をするので, バカが使うと青線で論文を書いてしまう.金はないが頭はあるヒト向け.
図が密かに 色が変わってるんだけど
draw.sh のスクリプト出しときましょう
#!/bin/bash
# PDEh.sh: 偏微分方程式I: 周期解
. draw.sh
. standards.sh
COLOR=1
X_AXIS='\fIX\sb\fR1\eb'
X_RANGE='0 1 0.25'
Y_AXIS='\fIu'
Y_RANGE='-1.25 1.25 0.5'
LINE=( Dash:Red:0.003 Solid:Blue:0.002 Solid:Green:0.003 Solid:Cyan:0.003 )
SYMBOL=( Omit )
OPT="--pen-colors=1=DarkRed:2=MediumSeaGreen:3=Blue:4=Magenta:5=GoldenRod3 --symbol-line-width 0.0020"
←これが, 色味を変えるコマンド. 色の名前はX11Colorですよ
#解析解のデータが,欲しい
seq 0 0|\
gawk '
BEGIN{pi=4*atan2(1,1);}
{
time=$1*0.5;
printf("#time= %f\n",time);
for(i=0;i<101;i++)
{
x=i/100;y=sin(2*pi*(x+time))^5;printf("%f %f\n",x,y);
}
printf("\n");
}
END{printf("\n");}' > $TMP/sol
cat > $TMP/legend.dat <<@
#m=Solid:Black,S=Omit
0.45 1. l:\fIt\fR = 1
0.65 1. l:CFL = 0.2
0.45 0.8 l:\fIi\fR-Sakurai scheme
#m=Dash:Red,S=Omit
0.1 -0.5
0.2 -0.5 l: theory
#m=Solid:Blue,S=Omit
0.1 -0.7
0.2 -0.7 l: \fIN\sbX\eb\fR\r8=\r820
#m=Solid:Green,S=Omit
0.1 -0.9
0.2 -0.9 l: 40
#m=Solid:Cyan,S=Omit
0.1 -1.1
0.2 -1.1 l: 80
@
LEGEND=$TMP/legend.dat
draw HD.pdf $TMP/sol PSOLVER_HD20.dat PSOLVER_HD80.dat PSOLVER_HD320.dat
こんな感じかな.
一番右は, 電機大の桜井先生のスキームですね.なめらかな関数には異様に強いんですよね・・・
初期値が違うとどうなんだ
違うって,値やら2階微分が不連続だったりするんっすよ.これは初期値のラムダ式を[](double x){return (x>0.8)?0:std::max(2.*x-0.6,0.);}とでもすればいいかな.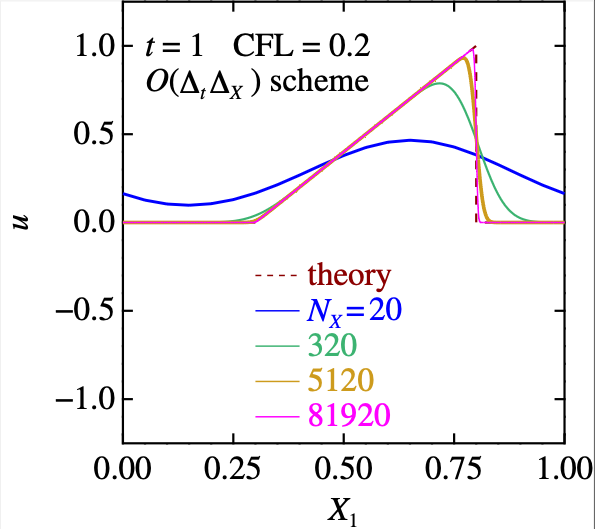
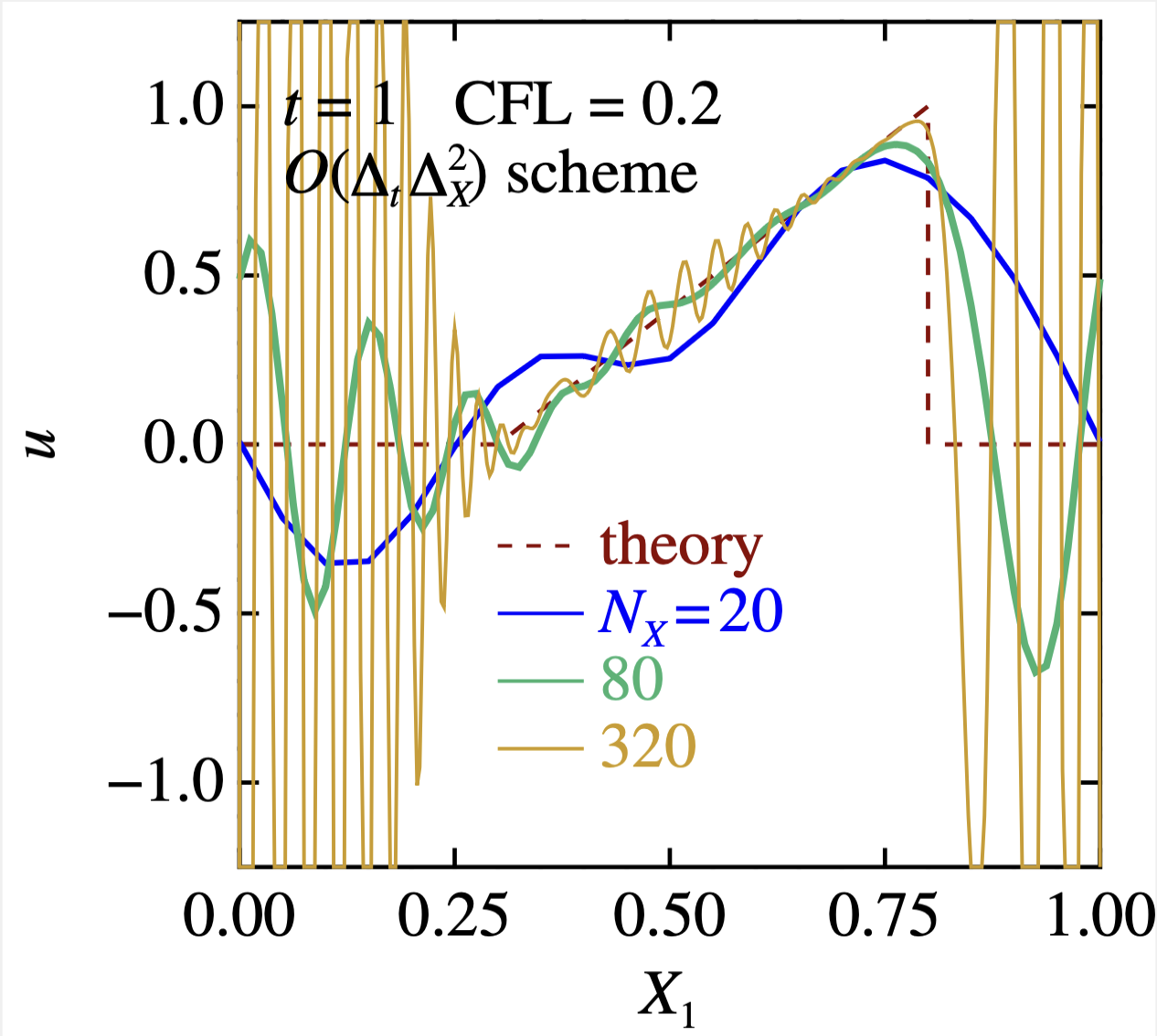
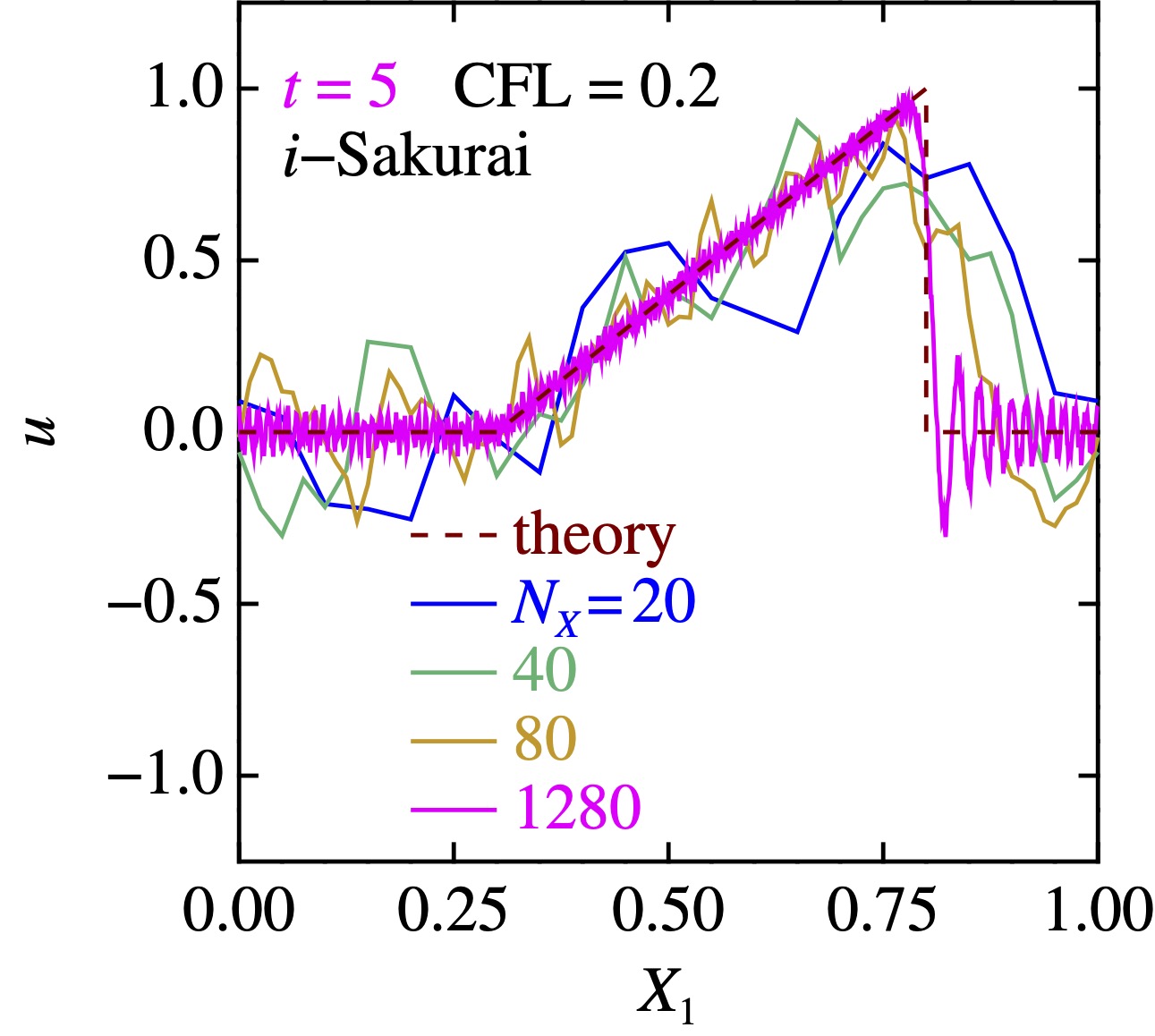
低精度スキームは, ダレダレですが,格子点数を超絶増やすと, 普通に解に近付いて行く.
- まあつまり,数値計算界では,力は正義であり,そしていつも正しい.
- 問題は・・・そんな大きな力が, 世界に一つも存在しないことが多い.ということだな
高精度スキームは, 格子点数を増やすと振動し始めて収拾がつかない.まあつまり,数値計算界では,力は正義であり,(工夫なしでは)おバカな方法が勝つ.
桜井先生のはまあ,発散はしないけど,程度だな.これでは使い物にならぬ.また後で考える
粘り気があると, どうなんだ
これは,最初にこっちを学んでからだな
差分の選び方がちがうと, どうなんだ
\(u_{i}\), \(u_{i-1}\), \(u_{i-2}\)の3点を用いる必要はない. \(u_{i+1}\), \(u_{i}\), \(u_{i-1}\)の3点を用いると, どうなるだろうか.
境界条件付きだと,どうなんだ
非同次項付きだと,どうなんだ
解析手法が違うと,どうなんだ
ここまで紹介した「差分法」が偏微分方程式を解く唯一の方法ではありません. 有限体積法を Levequeの教科書(うちの大学なら無料!)に基づいて紹介しましょう.
有限体積法
まず下図のように空間をセルに分割します:
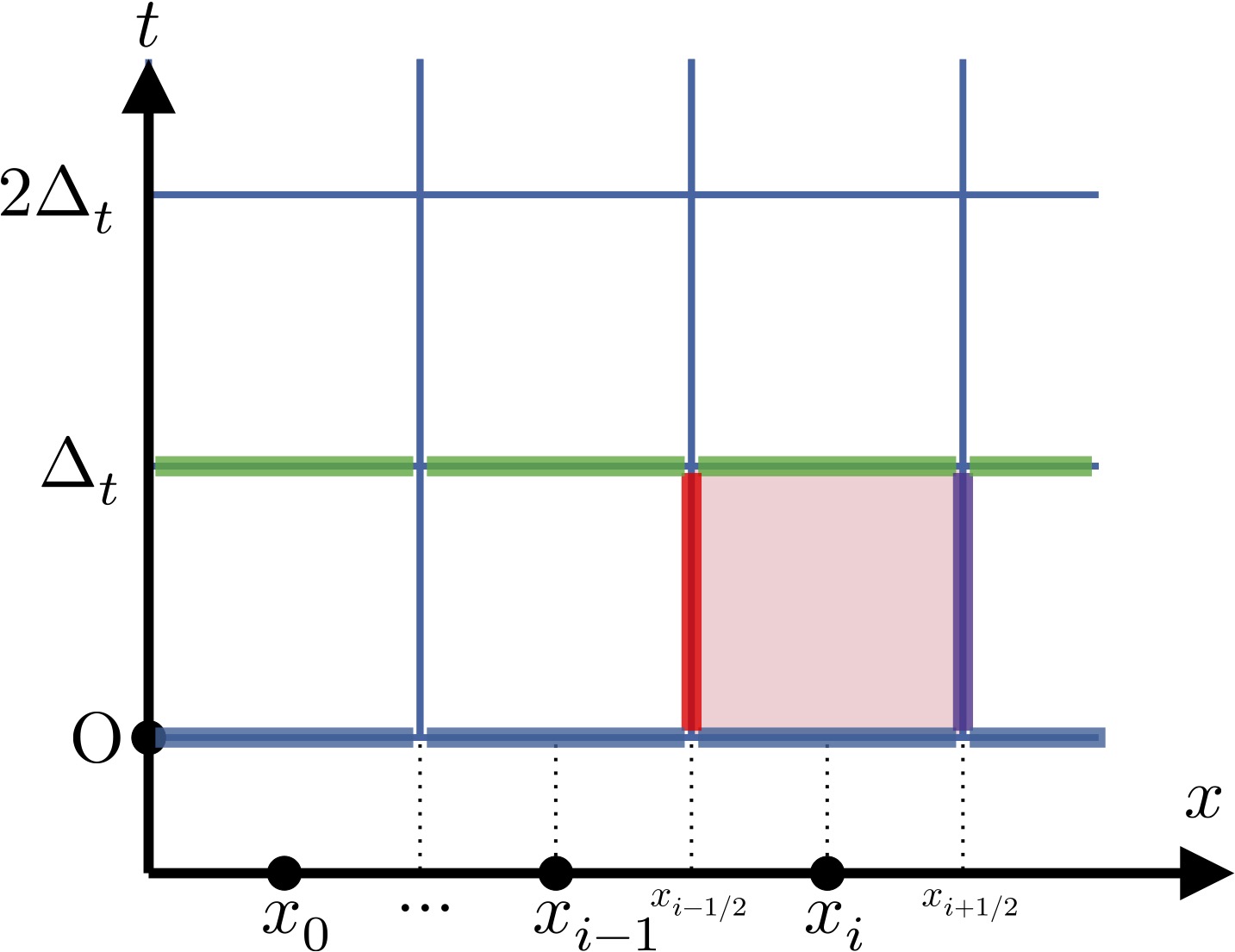
有限体積法では, 格子点上の\(u(t,x)\)の値ではなく, セル平均\[\bar{u}_{i}\left(t\right)=\dfrac{1}{\Delta_{x}}\int_{x_{i-1/2}<x<x_{i+1/2}}u\left(t,x\right)\mathrm{d} x\]の時間変化を追跡します(図の青色から,緑色が得られたらOK. 境界条件は足しても良いが, それ以外の情報は使わないことにする). そのために, 赤色の四角形内で方程式(1)を積分すると, \(u(t,x)\)が滑らかな関数であれば, \[\dfrac{1}{\Delta_{x}\Delta_{t}}\int_{x_{i-1/2}<x<x_{i+1/2}}\int_{0<t<\Delta_{t}}\dfrac{\partial u}{\partial t}\mathrm{d}t\ \mathrm{d}x=\dfrac{\bar{u}_{i}\left(\Delta_{t}\right)-\bar{u}_{i}\left(0\right)}{\Delta_{t}},\]\[\dfrac{1}{\Delta_{x}\Delta_{t}}\int_{0<t<\Delta_{t}}\int_{x_{i-1/2}<x<x_{i+1/2}}\dfrac{\partial u}{\partial x}\mathrm{d}x\,\mathrm{d}t=\dfrac{F_{i+1/2}-F_{i-1/2}}{\Delta_{x}},\]より, \[\bar{u}_{i}\left(\Delta_{t}\right)=\bar{u}_{i}\left(0\right)-\dfrac{c\Delta_{t}}{\Delta_{x}}\left(F_{i+1/2}-F_{i-1/2}\right)\tag{3}\]となります. ここに\[F_{\sharp}=\dfrac{1}{\Delta_{t}}\int_{0}^{\Delta_{t}}u\left(x_{\sharp},t\right)\mathrm{d} t\](あるいは, これに\(c\)を乗じたもの)を数値フラックスと呼びます. あとは, 青色データから,赤色や紫色のところの数値フラックスがわかれば, 時間発展を追うことができますね!
保存性について
物理では, \(u\)の総量は,系の総質量とか全エネルギーに対応することが多いので, \(u\)の総量が保存されることは重要です.方程式を見ても(境界周りは別の処理が必要ですが例えば周期領域\(0<x<L\)内の問題だと)\[\int_{0<x<L}\left(\dfrac{\partial u}{\partial t}+c\dfrac{\partial u}{\partial x}\right)\mathrm{d}x=\left(\dfrac{\mathrm{d}}{\mathrm{d}t}\int_{0<x<L}u\mathrm{d}x\right)+c\left[u\right]_{x=0}^{x=L}=0\]で変化しませんが,これは,有限体積法では, \[\int u\left(\Delta_{t},x\right)\mathrm{d} x=\Delta_{x}\sum_{i}\bar{u}_{i}\left(\Delta_{t}\right)=\Delta_{x}\sum_{i}\bar{u}_{i}\left(0\right)+C\sum_{i}\left(F_{i+1/2}-F_{i-1/2}\right)=\Delta_{x}\sum_{i}\bar{u}_{i}\left(0\right)=\int u\left(0,x\right)\mathrm{d} x\]のように\(i\)番目の右数値フラックスと\(i+1\)番目の左数値フラックスがキャンセルして, \(u\)の総量が原理的に保存する,という利点があります.
幸い,伝達方程式の解は特性線に沿ってConst.ですから,それぞれの数値フラックスの積分領域から時間を遡って, 初期データの積分に置き換えることができます!
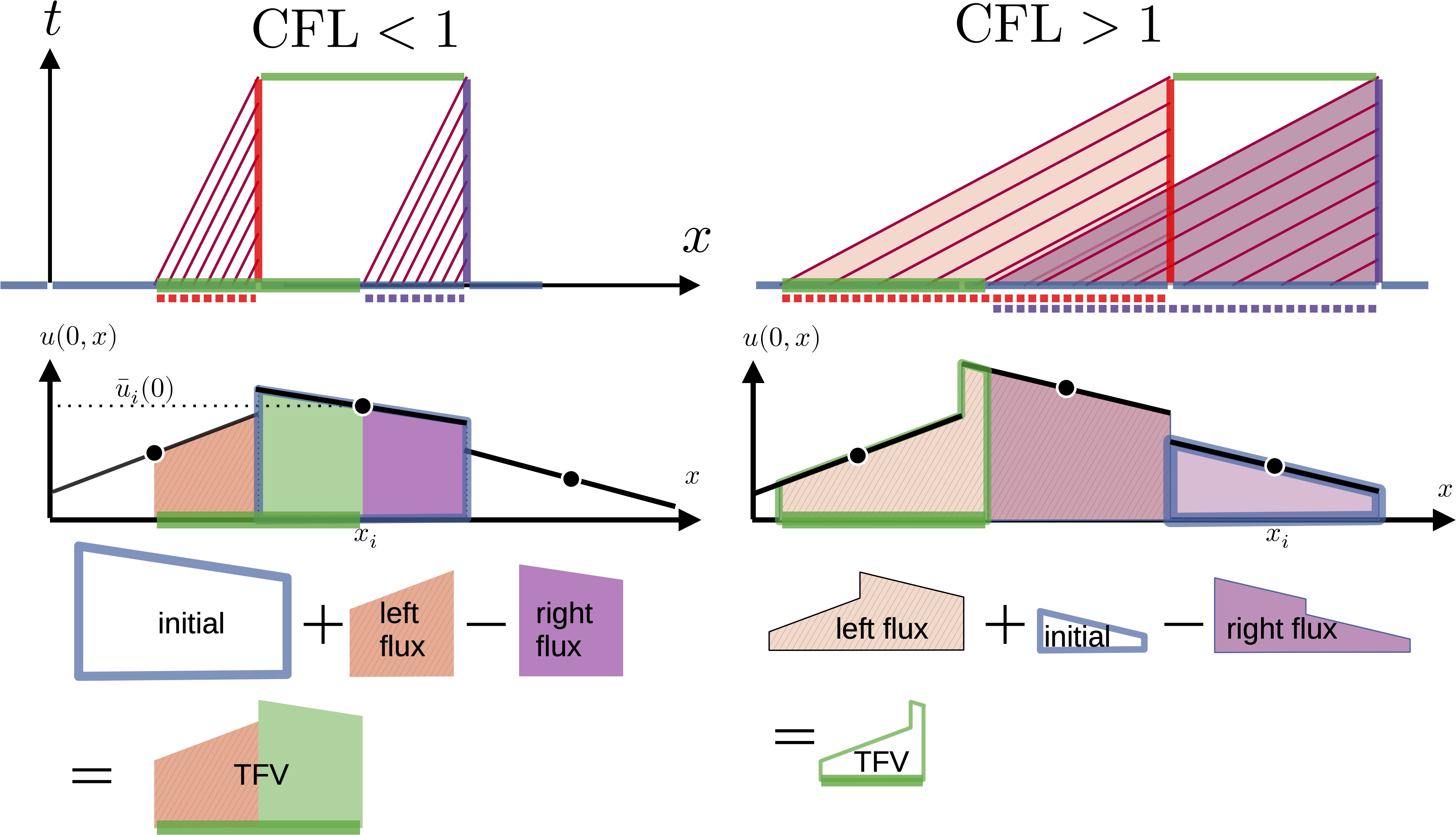
赤棒フラックス(左フラックス)は, 赤点線の範囲で, 紫棒フラックス(右フラックス)は,紫点線の範囲で積分することになります(世間ではCFL<1の場合しか説明してませんが,CFLは有限体積法と無関係のはずで, 積分範囲が増えるだけのはずです. もちろん,「数値フラックスを\(u_{i-1}\)と\(u_i\)だけから定めなければならない」と根拠レスな縛りをかけると, とうぜんCFL<1が必要になる).
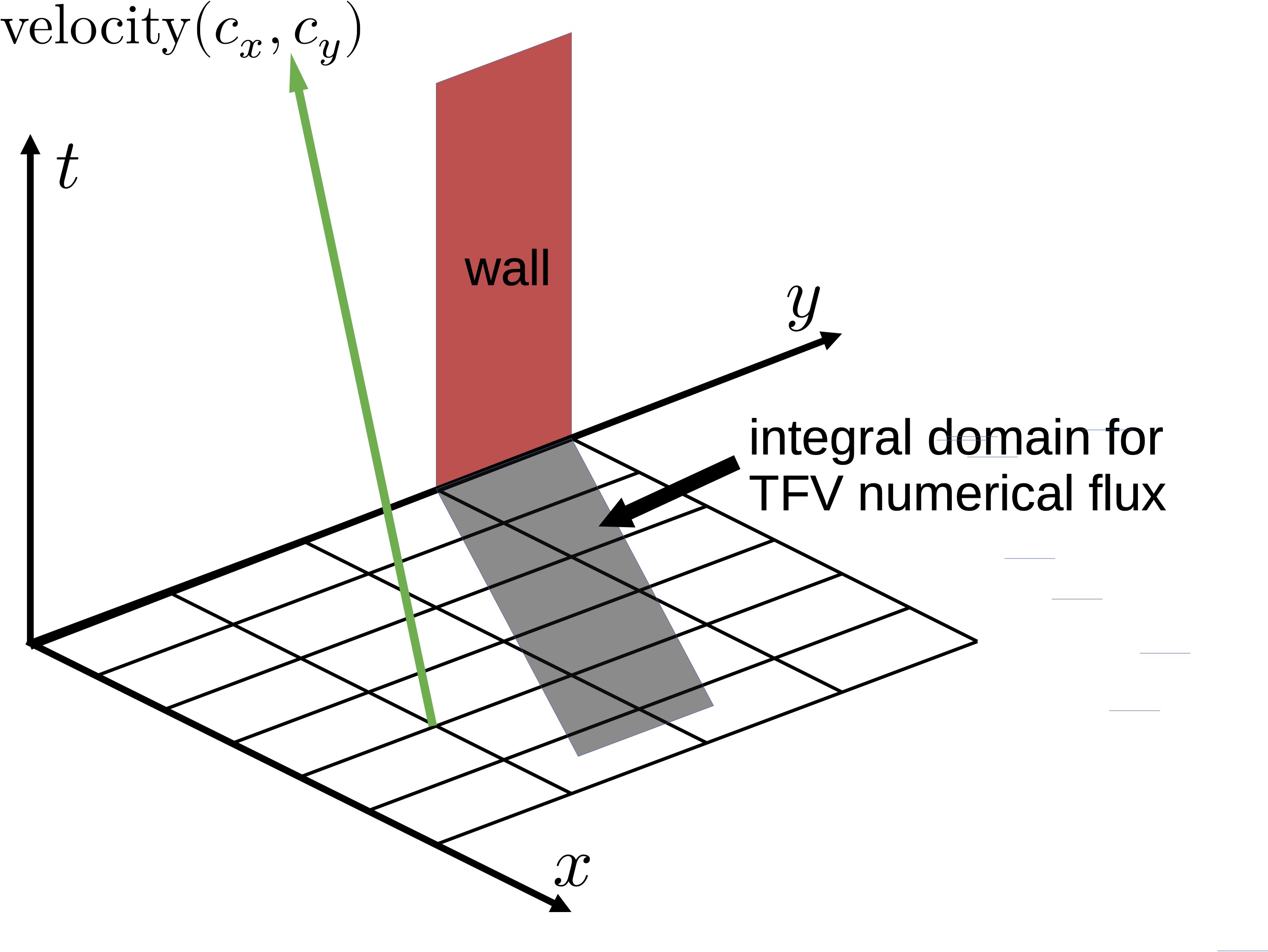 今は1Dだが, 2次元問題だったら,ここいらへんで積分する
今は1Dだが, 2次元問題だったら,ここいらへんで積分する
・・・のは面倒なのでxとyに分けたりすると, CFL<1 限定, 不連続不許可になっていくだろうね(いやそれ,CFLは無関係で\(\Delta_t\)の問題かもだが).
で,スペック上の誤差を小さくするには,\(t=0\)の関数をセルごとに適当な傾き\(\bar u^\prime_i\)を導入して,線形関数の該当領域を積分すれば良いです.
すると, (3)式は\[\bar{u}_{i}\left(\Delta_{t}\right)=\color{cyan}{\bar{u}_{i}\left(0\right)}+\color{red}{CF_{i-1/2}}-\color{magenta}{CF_{i+1/2}}\]となっているのですから,絵的に切ったり貼ったりして,依存領域(緑色の線)の積分を計算することになります.いやもう面倒だから,ダイレクトに緑色のとこ(移動してきた有限体積の場所)を計算してしまえ,ってのがコレです.
フラックスを計算した結果は, \(C<1\)の場合には.\[F_{i+1/2}=\bar{u}_{i}\left(0\right)+\dfrac{1-C}{2}\bar{u^{\prime}}_{i}\left(0\right)\Delta_{x}\tag{4}\]です. \(C>1\)の場合は無駄領域が多くて書き下すのが面倒なので,適当に計算してね.
あとは, 傾きをどう定めるか?ですね.これには色々流儀があります.
Lax-Wendroff
これは\[\bar{u^{\prime}}_{i}=\dfrac{\bar{u}_{i+1}-\bar{u}_{i}}{\Delta_{x}}\]と定めたものです.
Beam-Warming
これは\[\bar{u^{\prime}}_{i}=\dfrac{\bar{u}_{i}-\bar{u}_{i-1}}{\Delta_{x}}\]と定めたものです. なお, 中心差分みたいにしたのがFrommスキームです.
MinMod
説明を省きますが, Total Variationという概念があって, なぜかそれが良い方がいいという方針で作成した傾きもあります.MinModはその一つで,\[\bar{u^{\prime}}_{i}=\mathrm{minmod}\left(\dfrac{\bar{u}_{i}-\bar{u}_{i-1}}{\Delta_{x}},\dfrac{\bar{u}_{i+1}-\bar{u}_{i}}{\Delta_{x}}\right)\]とします. なお, \[\mathrm{minmod}\left(a,b\right)=\begin{cases}
a & \left(\text{if}\ |a|<|b|\ \text{and}\ ab>0\right)\\
b & \left(\text{if}\ |a|>|b|\ \text{and}\ ab>0\right)\\
0 & \left(\text{if}\ ab<0\right)
\end{cases}\]です.
有限体積用の 基底クラスを作成
格子とセルは1個数が違うので, オリジナルの基底クラスの,そこを訂正しましょう.
// pSolverFVBase.hpp Periodic soltuion by FV method using Cellwise Linear Reconsruction
#pragma once
#include "pSolver1DBase.hpp"
class FVKit
{
public:
double U; //セル内平均
double dU; //セル内勾配 ∂U/∂x
double RFlux; //右境界フラックス/c
FVKit &operator=(const double &x)
{
U = x;
RFlux = dU = 0;
return *this;
}
operator double() const { return U; }
};
class pSolverFVBase : public pSolver1DBase<FVKit>
{
protected:
void Grad2Flux() // Calculate Numerical Flux by Linear Reconstruction
{
for (auto &P : Data) P[nt].RFlux=P[nt].U+0.5*(1.-CFL)*P[nt].dU*dx;
}
public:
pSolverFVBase(const size_t &nx, const double &dt, const std::function<double(double)> &U0) : pSolver1DBase(nx, dt, U0)
{
std::cout << "Booting pSolverFVBase..." << std::endl;
// 格子点ではなくセルなので1個少ない
Data.resize(Data.size()-1);
Data.front().pre=&Data.back();
Data.back().next=&Data.front();
for (auto &P : Data) P.X += 0.5 * dx; // Xをせる重心に変更
}
void Initialize(void *parm=nullptr) override
{
std::cout << "pSolverFVBase::Initialize()" << std::endl;
}
virtual void getFlux()=0;
void Step(double U_W = 0.0) override
{
getFlux();
for (auto &P : Data)
P[nt+1].U = P[nt].U - CFL * (P[nt].RFlux - (*P.pre)[nt].RFlux);
time = (++nt) * dt;
}
};
差分だとUだけですが, フラックスとか, 傾きを保存できるようにパワーアップしましょう. で, ここは共通の(4)式を書いておきました.で, データを一個減らして,左右のアクセスを訂正しておきます.なお, back()は配列の最後の要素の参照,front()は配列の最後の要素の参照なので,こうやって繋いでおくと周期配列になります.
数値フラックスの計算は,傾きの計算に依存するので,このクラスを派生して実装しましょう.このへんは, (3)式を実装しています.で,これを実行する前に,ここでgetFlux()関数で傾きを計算しておけばOK,という寸法だ.
実際の スキームは,まあ 色々だが みんな同じだ
例として, MinModのやつを示しておきましょう:
// pSolverFVMinMod.hpp TVD periodic Finite Volume with MinMod Gradient
#pragma once
#include "pSolverFVBase.hpp"
class pSolverFVMinMod : public pSolverFVBase
{
double MinMod(const double a,const double b)
{
if (a*b<0) return 0.;
if (std::abs(a)<std::abs(b)) return a;
return b;
}
public:
pSolverFVMinMod(const size_t &nx, const double &dt, const std::function<double(double)> &U0 = [](double x)
{ return 0.; }) : pSolverFVBase(nx, dt, U0)
{
std::cout << "Booting pSolverFVMinMod..." << std::endl;
}
virtual void getFlux() override
{
for (auto &P : Data)
{
auto& L=*P.pre;
auto& R=*P.next;
P[nt].dU = MinMod(P[nt].U - L[nt].U,R[nt].U-P[nt].U)/dx;
}
Grad2Flux();
}
};
もはや説明するC++文法はないな. まあここくらいか.これは派生クラスで定義されてないので,pSolverFVBaseクラスで定義したやつが実行される.
main()
まあmain()の例
// main.cpp
#include <iostream>
#include "pSolverFVMinMod.hpp" //MinMod-Limitter
int main()
{
size_t nx = 20; // 空間分割数 100(text), 40, 20, 8
double dt = 0.8 / nx; // 時間刻み幅 CFL=0.8 に固定しとこ. つまり 0.2/40
size_t ntmax = 5. / dt; // 最大時間ステップ数
size_t ntsave = 5. / dt; // データ保存間隔
auto I_SIN = [](double x)
{ return std::pow(std::sin(2.0 * M_PI * x), 5); }; // 初期条件として正弦波^5を設定
auto I_LEVEQUE = [](double x)
{
double b=200;
double xc=x-std::floor(x+0.2)-0.3;
double y=exp(-b*xc*xc);
if ((xc>0.3)&&(xc<0.5)) y+=1;
return y;
}; // Lebequeのテキストの初期関数
auto I_DC = [](double x)
{ return (x > 0.8) ? 0 : std::max(2. * x - 0.6, 0.); };
//--------------------------------------------------
std::string filename = "Data/test03/TEXT_FVMM20.dat";
pSolverFVMinMod mySolver(nx, dt, I_LEVEQUE);
//--------------------------------------------------
mySolver.Initialize();
for (size_t nt = 0; nt < ntmax; nt++)
{
mySolver.Step(); // 時間ステップを実行
if ((nt + 1) % ntsave == 0)
mySolver.Write(filename);
}
return 0;
}
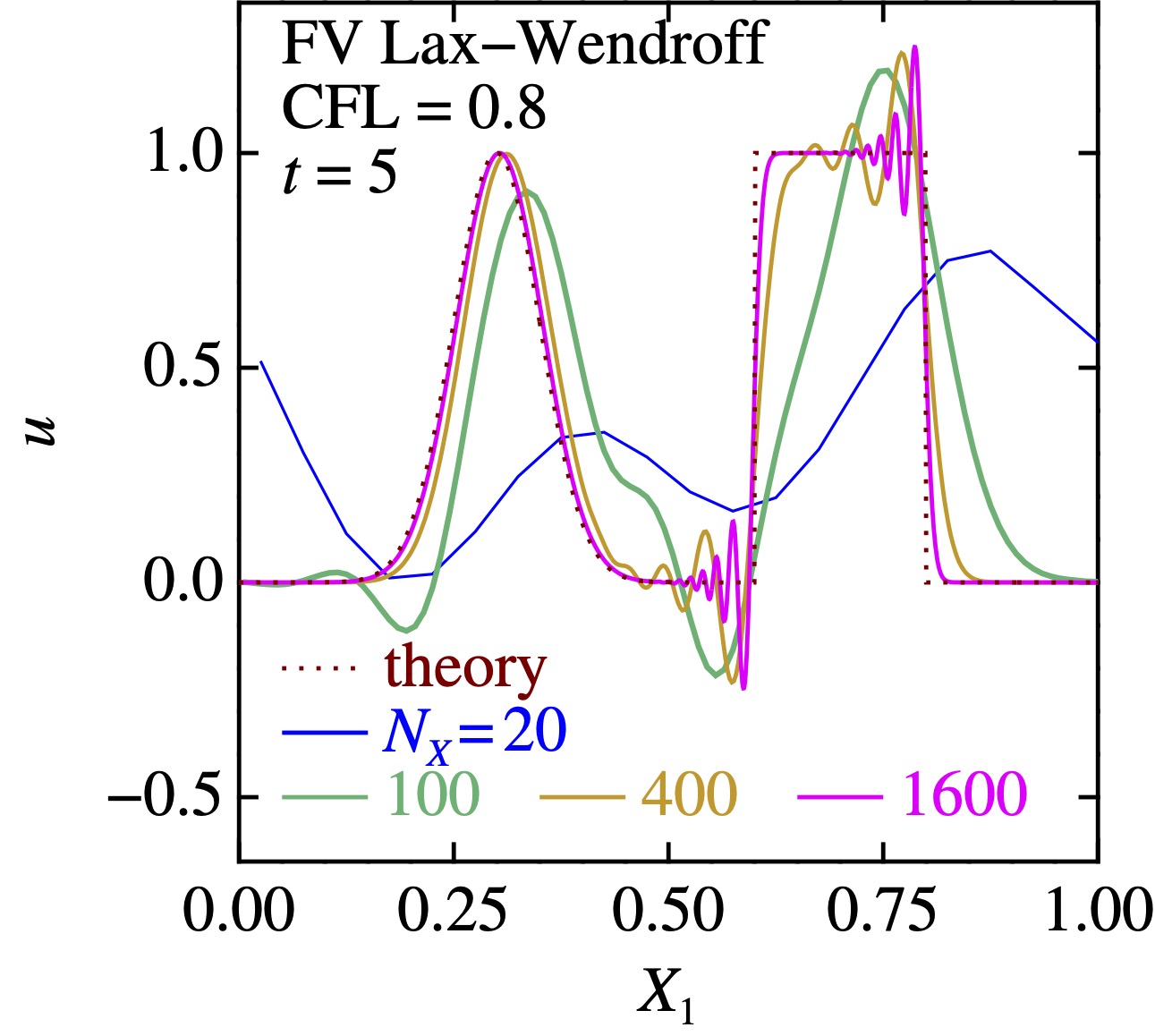
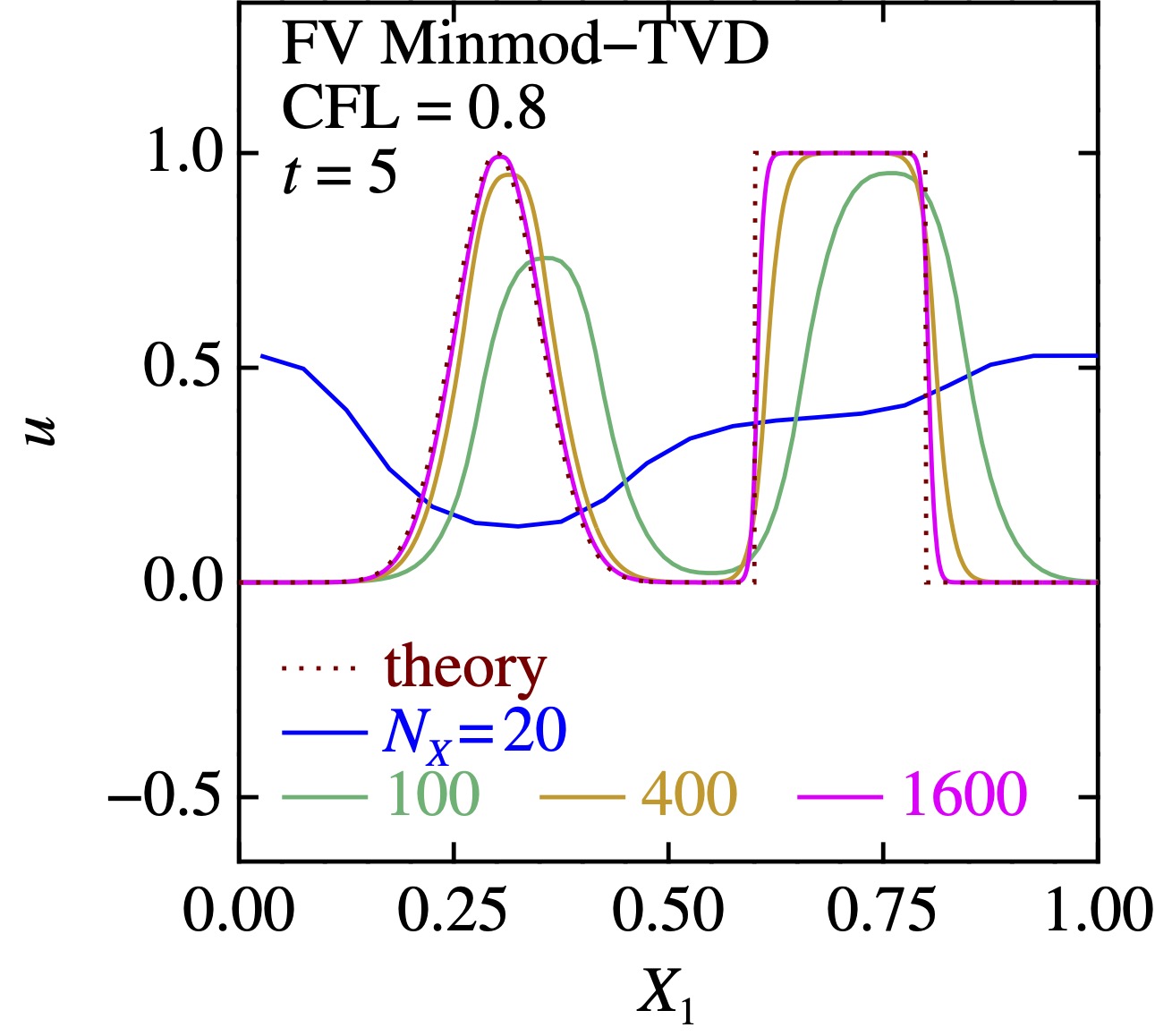
ここで定義しているラムダ式は, Levequeの教科書(うちの大学なら無料!)に記載されている例である.
結果はこんな感じになる: