境界値問題

\(x=0, 1\)において, 境界条件\[ y(0)=1,\quad y(1)=0\]が与えられている場合は, どうしましょうか. この場合には, 2階微分に対する差分式\[\frac{\text{d}^2 y}{\text{d}x^2}\approx\frac{y_{i+1}-2y_i+y_{i-1}}{\Delta x^2}\]を連立させて解くことができます. すなわち \[ \begin{bmatrix}2-C\Delta^{2} & -1\\ -1 & 2-C\Delta^{2} & -1\\ & -1 & 2-C\Delta^{2} & -1\\ & & \ddots & \phantom{2-}\ddots\phantom{2-} & \ddots\\ & & & -1 & 2-C\Delta^{2} & -1\\ & & & & -1 & 2-C\Delta^{2} \end{bmatrix}\begin{bmatrix}y_{1}\\ y_{2}\\ y_{3}\\ \vdots\\ y_{N-2}\\ y_{N-1} \end{bmatrix}=\begin{bmatrix}y_{0}\\ 0\\ 0\\ \vdots\\ 0\\ y_{N} \end{bmatrix}\tag{1}\]を解けば良いわけですね! 面倒だから\[\mathsf{A}\boldsymbol{y}=\boldsymbol{b}\]としておきましょう. こういう, 真ん中3行だけの行列を, 「三重対角行列」と呼びます．

あとは行列をいかに解くか? という問題に帰着します.

現代では，とりあえず願ってみましょうね

うむ．まあできておるが，文法要素をもう少し入れ込んで改造ますね！

ベクトル\(\boldsymbol{y, b}\)

まず多次元のベクトルが必要です．これは配列データに格納しましょう. C++の配列は std::vector を用います.

#include <vector>
...中略...
std::vector<double> b;

bに多数の double (浮動小数点数)の値を格納できます．

b.resize(100);

で, 100個の値を格納できるようになります. めちゃくちゃ初心者が間違えるのは, 先頭がb[0]であることです. (1)式ではb[1]...b[N-1]でN-1個あるのです．

b.resize(N-1);

で良いのですが, 1行目はb[0]で，最後の行はb[N-2]です. 最初が0なので1ずれることに注意してください. 例えば

b[N-1]

はN番目の値です. N-1個しかないのにN番目にアクセスすると, 運が良ければコンピュータがエラーして停止します. 大抵の場合, コンピュータはエラーせずに計算が終了し, 最終結果として誤った結果が得られます. あんた間違ってるよ，とかは決して言ってこない. で，それを論文に投稿してしまい，「こいつ，嘘つきで賞」を貰えます. こういうのを, バグといいます.

嘘つくつもりはなかった, という言い訳が通るほど世間は甘くありません．間違える奴＝嘘つき→雑用係です．

初心者のうちは, これが恐ろしいのですが, b[i] の代わりに

b.at(i)

を用いて書くと, 範囲内であるかどうかをいちいちチェックしながら計算しますので，バグに遭遇するとコンピュータがエラーして停止します. コンピュータがエラーを出さなければ最終結果は正しいでしょう．ただし，毎回チェックしながら計算を行うので，計算速度はかなーり遅くなります.

行列\(\mathsf{A}\)

行列は, double1個では入れられませんね. ここでは「1行」を表す内部クラスを作成してみましょう. こんな感じです:

#pragma once    //ifdef...とかしなくても, 現代では，これで行けるらしいな
#include <iostream>
#include <fstream>
#include <vector>
#include <cmath>

class BC_Solver {
public:
    double C=1.0;
    int N = 100;
    double Xmin = 0.0;
    double Xmax = 1.0;
    double Y0 = 0.0;      // 左端の境界条件
    double Y1 = 0.0;      // 右端の境界条件
    std::vector<double> y;
    double dx;
    void Solve(){
        dx=(Xmax-Xmin)/N;
        std::vector<double> b;
        b.resize(N-1);              //方程式の数だけ確保
        y.resize(N+1);              //境界条件で２個追加
        class ROW {
        public:
            double L,C,R;           // 左列,中列,右列
        };
        std::vector<ROW> A(N-1);    //要素数を最初から定義しても良い
        for(auto& row:A) {  row.L=-1.;   row.C=2.-C*dx*dx;  row.R=-1.;}
        // 境界条件
        for(auto& v:b) v=0;
        b[0] = Y0;
        b[N-2] = Y1;
        ....
    }
    void Save(std::filesystem::path file){
    ...

これは僕も今初めて知りました. AI万歳. この辺が, 上で説明したvectorです.　Solve()とSave()で，どちらでも必要な y および dx は，ここいらでメンバー変数に定義．次に行列を定義しよう．

内部クラス

ここでふっとクラスの定義が始まってます．行列の1行とは，どのようなものか，を定義しています. 左と真ん中と右に, double が一個づつあることを表してます. この行がたくさんあって，行列になるわけです. で, std::vectorは, 相手がなんであろうと，配列にできることも重要です．

さて，クラスの定義というのは，よそで使う予定がないのであれば, この例のように，必要なところにふっ，とかけます．これを内部クラスと言います. 計算速度の点では, 「必要になるところで，ふっと，変数を定義する」方が，高速になります．Fortranのように「プログラムの先頭で変数を定義」する流儀との違いを説明しましょう.

プログラムの先頭で変数を定義したとする．
- その変数は，広大なプログラムの，どことどこで，利用されるかわからない．ある場所で計算し，はるか遠くで，その値を利用する可能性が否定できない．
  - 両者の間で, 共通の，変数の値を保存しておかなければならぬ.
  - つまり，値を保持できる「メインメモリー」に配置する．読み書きが遅くなるけど，変数の値が途中で消えるよりはマシ
必要なところで，ふと定義した変数は，{ } の外部では，利用できないため，利用されないことが確定している
- 使った後，値を保存しておく必要はない．利用後直ちに廃棄すれば良い
  - ならば, 高速なCPUのキャッシュメモリーに配置しよう. メインメモリーには保存しないので，次回とか別の計算で，その値を思い出して使うことはできないが，その必要がない
  - 計算が超高速なので，良いはずだ

現代ではメインメモリーとキャッシュメモリーの速度差は2桁近いので，用もないのにメインメモリーを使うのは損です．

範囲指定For文

ここは，「Aの要素全てに，これを行え」というfor文です．数えなくていい時には，このように書きます．auto& はのちに説明します．& を忘れないように注意！

row ってのが, Aの各要素（ROWクラスのインスタンス）を表すわけです. で, rowのメンバー L, C, Rに値を設定できます.

これで，次のように定義できたことになります:
\[
\begin{bmatrix}b_{1} & c_{1}\\ a_{2} & b_{2} & c_{2}\\ & a_{3} & b_{3} & c_{3}\\ & & \ddots & \ddots & \ddots\\ & & & a_{N-2} & b_{N-2} & c_{N-2}\\ & & & & a_{N-1} & b_{N-1} \end{bmatrix}
\begin{bmatrix}y_{1}\\ y_{2}\\ y_{3}\\ \vdots\\ y_{N-2}\\ y_{N-1} \end{bmatrix}=\begin{bmatrix}b_{1}\\ b_{2}\\ b_{3}\\ \vdots\\ b_{N-2}\\ b_{N-1} \end{bmatrix}\]\[
\qquad\Longleftrightarrow\qquad
\begin{bmatrix}
\mathsf{A[0].C}&\mathsf{A[0].R}\\
\mathsf{A[1].L}&\mathsf{A[1].C}&\mathsf{A[1].R}\\
&\mathsf{A[2].L}&\mathsf{A[2].C}&\mathsf{A[2].R}\\
& & \ddots & \ddots & \ddots\\
& & &\mathsf{A[N-3].L}&\mathsf{A[N-3].C}&\mathsf{A[N-3].R}\\
& & & &\mathsf{A[N-2].L}&\mathsf{A[N-2].C} \end{bmatrix}
\begin{bmatrix}\mathsf{y[1]}\\\mathsf{y[2]}\\\mathsf{y[3]}\\ \vdots\\\mathsf{y[N-2]}\\\mathsf{y[N-1]}\end{bmatrix}=
\begin{bmatrix}\mathsf{b[0]}\\\mathsf{b[1]}\\\mathsf{b[2]}\\ \vdots\\ \mathsf{b[N-3]}\\\mathsf{b[N-2]}\end{bmatrix}
\]

\(i=1\)行目から\(N-2\)行目まで, \(i-1\)行の定数倍を\(i\)行目に加えて, \(\mathsf{A.L}\)の要素を0にできます.　もちろんそのとき\(\mathsf{A.C}, \mathsf{b}\)も変わってしまいますが, 計算機ですので計算するようにプログラムできます．これを繰り返すと，行列は次のようになります:
\[
\begin{bmatrix}
\mathsf{A[0].C}&\mathsf{A[0].R}\\
\mathsf{0}&\mathsf{A[1].C}&\mathsf{A[1].R}\\
&\mathsf{0}&\mathsf{A[2].C}&\mathsf{A[2].R}\\
& & \ddots & \ddots & \ddots\\
& & &\mathsf{0}&\mathsf{[A[N-3].C}&\mathsf{A[N-3].R}\\
& & & &\mathsf{0}&\mathsf{A[N-2].C} \end{bmatrix}
\begin{bmatrix}\mathsf{y[1]}\\\mathsf{y[2]}\\\mathsf{y[3]}\\ \vdots\\\mathsf{y[N-2]}\\\mathsf{y[N-1]}\end{bmatrix}=\begin{bmatrix}\mathsf{b[0]}\\\mathsf{b[1]}\\\mathsf{b[2]}\\ \vdots\\ \mathsf{b[N-3]}\\\mathsf{b[N-2]}\end{bmatrix}
\]
そしたら, 　y[N-2]から順に解けますよね！こんな感じです:

// 境界条件
for(auto& v:b) v=0;        b[0] = Y0;        b[N-2] = Y1;
//前進消去
for(int i=1;i<N-1;++i) {
    auto m=A[i].L/A[i-1].C;
    A[i].C -= m * A[i-1].R;
    b[i]   -= m * b[i-1;
}
y[N]=Y1;
for(int i=N-1; i>0; --i)
  y[i]=(b[i-1]-((i<N-1)?: A[i-1].R*y[i+1] : 0.0 ))/A[i-1].C;
...

この auto というのは何か？ここは正確には double と書くべきで，それは学習済み「double 変数 m , 召喚」という意味でした. でも, 召喚するべきものが神なのか悪魔なのかは, = の右側を見ればわかるので, 無駄です．今回の場合，明らかに，ここはdouble型の数値になってます．このように, 変数を見たら自ずから変数型がわかる場合, auto と書いて良いのです．書くのが，面倒くさいからです．for文の書き方も，一箇所新項目ですね．こういうふうに，減らしながら数えても良い.

この謎構文は，条件文？真の場合：嘘の場合というものです．ここでは i < N-2 であれば, A[i].R*y[i+1] になり, i=N-2 であれば, 0 になります．多用すると，読みにくいので気をつけよう．

データを保存する関数も, 書いておきましょう．今回は, Save(ファイル名)という感じにしてみました:

   ...
}
void Save(std::filesystem::path filename){
    std::ofstream ofs(filename);
    for(int i=0; i<= N; ++i) ofs << i*dx << " " << y[i] << std::endl;
    ofs.close();
}

簡単ですね！でも，簡単すぎて「filenameを構成するフォルダー名の中に，まだ作成していないフォルダーが含まれてたら，エラーする」だろうな〜と思って試したら，仕様上は，フォルダー Data/test03 が存在しない場合，エラーも表示せず，データも作成しない，困ったプログラムになりました！フォルダーの存在をチェックしないお前が悪い．エラーではない，のだそうです．AIモンキーに言わせると，「そりゃフォルダーが存在する場合も，しない場合も，いつでも下ので良いので普通にそう書くやろ？」だそうです. 初めて知りましたわ・・・

   ...
}
void Save(std::filesystem::path filename){

    std::filesystem::create_directories(filename.parent_path());
    std::ofstream ofs(filename);
    for(int i=0; i<= N; ++i) ofs << i*dx << " " << y[i] << std::endl;
    ofs.close();
}

計算結果

で，これを計算すると, こんな感じになります(\(C=200, N=20, 40\)としてみた):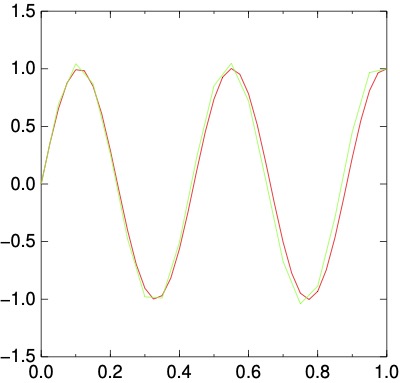

Jacobi法

連立方程式\[\text{A}\boldsymbol{x}=\boldsymbol{b}\]の解法には, 逐次近似法というものがあります. 行列\(\text{A}\)の対角成分を\(\text{D}\)とおき, \[\text{B}=\text{A}-\text{D}\]と定めると, 連立方程式は\[\text{D}\boldsymbol{x}=\boldsymbol{b}-\text{B}\boldsymbol{x}\]となります. Jacobi法では, 気分で定めた初期ベクトル\(\boldsymbol{x}^{(0)}\)から, 漸化式\[\text{D}\boldsymbol{x}^{(i)}=\boldsymbol{b}-\text{B}\boldsymbol{x}^{(i-1)}\]によってベクトル列\(\boldsymbol{x}^{(i)}\)を定めると, あらあら不思議，かなり多くの場合に解に収束するというものです.

Jacobi法の物理的イメージは熱方程式のセクションで説明することにして, 実際にやってみましょう．

上と同じように，3列だけ保存するのが正解ですが，行列演算の練習を兼ねて，三重対角行列であることを忘れて，密行列として計算プログラムを組んでみます．

例えば\(N=40000\)のように営業サイズの分割数になると, 非常に大量のメモリーを消費しますので，気を付けてください．具体的には，double 変数は1粒で8byte消費するので, 本当に必要なメモリーサイズは, 行列が3列, 解が1列, ベクトル1列で\(5N\)個あるので, \[\frac{8\times5N}{10^9}\approx 0.0016 \text{GB}\]であるのに対し，密行列には\(N^2\)個の要素があるので, プログラムが消費するメモリーは\[\frac{8\times(N^2+2N)}{10^9}\approx 12 \text{GB}\]となり，大抵のデスクトップPCを暴走させるのに十分なサイズになってきます．つまり，うっかり密行列で解こうとした人には, 大変難しい問題に見えるわけです．正しい取扱いを行なった同業者には，なんの困難もない，ということになります．

消費メモリーサイズが計算機のメモリーサイズを超えると，計算速度は恐ろしく低下します．10秒で済むものが1週間かかったりします．コンピュータは「メモリーが足りませんよ」と連絡してくることはありません．あなたが，確認する必要があります．ここでは，消費メモリーサイズを確認する方法も覚えましょう．

線形代数ライブラリを使う

密行列を取り扱うのは, Eigenライブラリーを用いるのが簡単です（Eigenは疎行列も扱えます．念のため）．

Eigenはとにかく計算が段違いに早いです．まずはここに従ってインストールを済ませましょう.

注意: Eigen-3.4.0以降でなければ, C++20でエラーが起こります．

先のプログラムに, 別解法ということで別のファイルをつけてみましょう

　Jacobi.hpp をつけてみた

で, さっきのBC_Solverではなく Jacobi したいので，メインプログラムを

#プリプロセッサ

ちょっと古い方法ですが, 「プリプロセッサ」を使ってみています. 具体的には

#undef  USE_JACOBI      ←これで, USE_JACOBIスイッチがOFF. とはいえ，デフォルトでスイッチはOFFなので意味なし
#define USE_JACOBI      ←これで, USE_JACOBIスイッチがONになる
.....
#ifdef USE_JACOBI
    スイッチONの時のプログラム
#else
    スイッチOFFの時のプログラム．今回の場合，さっき作った BC_Solverクラスを使うプログラム
#endif
    return 0;
}

スイッチのON/OFFで, 複数通りのプログラムを入れておけます. プログラムを書いていると

Windowsだと, こう書かなければならぬ
Macだとこれ
スパコンだと，こっちしかダメ

とかいう，腐った事情に遭遇することがあります．そう言うときに，スイッチ一発でかき分けられる. 今回は，「別のプログラムに書いたら良いんじゃね？」的な問題なので，使わなくても良いのですが，お勉強なので，試しに使ってみましょう.

ま，#ifdef, #else, #endif, #define, #undef, #include, #pragma 以外は使わないな．#pragma はここらで並列計算するときに説明します．

Eigen続き

\(N\times N\)の行列を準備し，係数行列にするには次の通り：

#include <Eigen/Dense>
class Jacobi
{
private:
  Eigen::MatrixXd myMAT;
  Eigen::VectorXd myVEC;
  ...中略...
public:
  Jacobi(){std::cout << "ういーっす" << std::endl;}
  void resize(size_t N){
    myMAT.resize(N-1,N-1);
    myMAT.setZero();
    myVEC.resize(N-1);
    myVEC.setZero();

    ....

赤色部分がそれぞれ行列とベクトルの宣言です．Xdは浮動小数であることを意味しています．次元は青色のところで設定しています．setZero()をしないと，要素が0になりませんので注意してください. 使い方には特に注意はないです．数学とは異なり, 添字が0からですので注意. 添字は[i]と書いても(i)と書いても同じですが, (i)は範囲チェックを行いますので, 計算は安全ですが遅いです．

さて, 英文でJacobiクラス, なので, Solve()と書いたら先を読まれます:

なるほど・・・では， AIが書いたプログラムをもとに, 書いていきましょう.

行列要素の初期化

どうやらAIは, myMAT行列に係数が既に用意されている，という想定でプログラムを書いたようなので, 係数を用意して差し上げます. Init(){ と入力すれば，外形を作ってくれたので，それを修正するだけ.

ドキュメントの整形

プログラムのバグを少なくするには，「見た目が美しい」ことが重要です．あなたが書いても美しくはならないので，書いた範囲を選択して【ドキュメントのフォーマット】を行いましょう：

とはいえ，ほとんど先を読まれて修正箇所なし

Eigenのパワーを楽しむ

Eigen行列には色々なオペレータが定義されているので，便利に使ってください．例えば inverse() は逆行列を与えます．ので，

void Inv()
{
  auto SOL=myMAT.inverse()*myVEC;
  mySOL[0]=Y0; //これは境界条件
  for(int i=0;i<SOL.size(); ++i) mySOL[i+1]=SOL[i];
  mySOL[mySOL.size()-1]=Y1;
}

これで問題ない. もちろん答えは出る. main()関数で, resize()→Init()→Inv()の順で呼び出すだけ！

・・・まあしかしなんというか，\(N\)が1000とか10000になると, 逆行列の計算はまぢ遅いので，あまり実用しないほうが良いです(逆に言えば，それ以下なら，これが一番早い)．実際，N=12000で走らせてみると，だいたい \(12000^2 \times 8 /1024/1024/1024 \sim 1 \)GB以上のメモリーを使うはずである. せっかくなので, プログラムのメモリー使用量を知る方法を覚えよう.

topコマンド

ターミナルで top と入力する. これは, Linuxなど計算機クラスターでも, 同じものが使える.

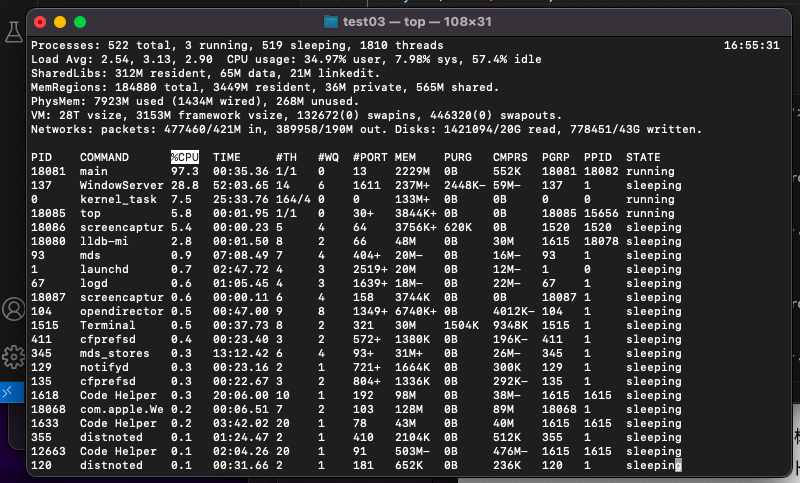　あなたのプログラム main が 97%のCPU, 2200MBのメモリーを使っていることがわかる.

ActivityMonitor

MacのActivityMonitorは，かすかに見やすいかも

Jacobi法のプログラム

AIが作ったJacobi法プログラムを見てみよう. ．

void Solve(size_t max_iter = 10000)
{
        size_t message_iter = 1000; // 途中で「XX回やったよ〜」とメッセージを出したい
        double tol = 1e-10;         // 途中でもズレがこの値になったら中断して良いことにする（収束限界）
        Eigen::VectorXd x_old = myVEC;
        Eigen::VectorXd x_new = myVEC;
        x_old.setZero();                  // Eigenベクトルを0ベクトルにする
        x_new.setZero();
        // 初期化
        size_t iter = 0;
        double err = 1.0;
        while (iter < max_iter)
        {
            iter++;
            for (int i = 0; i < myMAT.rows(); ++i)    //  行列 A と ベクトル　x_old の積を計算する
            {
                x_new[i] = 0.0; // 初期化
                for (int j = 0; j < myMAT.rows(); ++j)
                    if (j != i) // 対角要素を除く行列積
                        x_new[i] += myMAT(i, j) * x_old[j];
                // D * x_new = b - (A-D)*x_old   対角行列だから割れば良い
                x_new[i] = (myVEC[i] - x_new[i]) / myMAT(i, i);
            }
            if ((err = (x_new - x_old).norm()) < tol)
                break;
            x_old = x_new;
            if (!(iter%message_iter))
                std::cout << "Iteration " << iter << ": Error = " << err << std::endl;
        }
        if (iter == max_iter)
            std::cout << "Timeout. Error= " << err << std::endl;
        else
            std::cout << "Converged in " << iter << " iterations." << std::endl;
        for (int i = 0; i < myMAT.rows(); ++i)
            mySOL[i + 1] = x_new[i];
}

あれ．ここは関数の引数であるですが, なんか知らんが，初期値が代入されてますね．これは，省略可能な引数で，Solve(214)と起動したら max_iter=214 で開始するのですが, Solve() と起動したら max_iter=10000で開始するのです．

この辺は, Eigenのベクトルを0ベクトルにする命令です.

このwhile (条件式)ってのは, 条件がtrueである限り, その下の行({}があったら，そいつ)を繰り返せ，という繰り返し文の書き方です．このやり方の時には, 途中で iter++ とやってる感じで，いつか条件がfalseになるように仕込んでおく必要があるので注意ね！

この辺は, 行列とベクトルの席を計算しているだけですね！A-Dを計算する代わりに, i行j列で, i=j ならスキップしろ！と書いています．

ここは解説が入りますね！x_oldとx_newは, Eigenのベクトルで，引き算した結果は Eigenのベクトルです（変数名は無いが，変数の型はある）．すると，そのクラスの関数は利用できるのです！norm()は, ベクトルの大きさの平方根です．で，それが小さな数 tol よりも小さかったら，収束したと判断してwhileなどのループを中断する命令 break を出します．

breakは, 最も内側のループを中断します．例えば

for(.....)
{
   while(....)
   {
      for(....)
      {
         ....
         break;
         ぱおぱお;
      }
　　　 にゃーん;
   } // whileループ終わり
}

であれば，中断するのは赤色のループであって，ぱおぱおは実行されず，にゃーんが実行され, whileループは実行継続です．

この条件文も説明が必要ですね！まず A%B というのは, AをBで割ったあまり(mod)です．なので, iterをmessge_iter=1000で割った余りが0のときだけ（要するにiter=1000,2000,...で）進行状況を画面に表示しよう，という作戦です．だったら if (iter%message_iter==0) で良いのですが，C++のif文には面白い性質があり, if (整数の0) はfalseで実行せず, if (整数の0ではない数) なら実行するのです．そこで, 論理否定「！」を前につけて, !( 割り切れたら0) つまり (割り切れなかったら0) に変更してif文を行なってます．

さらに, （）を省いて ! iter % message_iter としてはダメです．このとき, ! iter は「iterを二進数表記にして0101110001とかにしてから」「！で0と1を反転」という，全然違う命令になってしまうからです．こういうふうに，「演算の優先順位」は，小学校で 1+2x3 が 9 ではなくて, 7 だよ！と教えてもらった時と変わらず，重要です！不安に思ったら, () を利用しましょう．

実行してみる

では, main()を適当に書いて実行してみた. 注意すべきことは, (1)の行列の要素を見て分かるように, \[ 2 - C\Delta^2 >0 \]でなければ，まずそう！ということである. Jacobi法のような「逐次近似法」は，神のご加護があれば収束するが，必ず収束するわけではない．神のご加護を理解するには，数学的にどうなのかを調べないとね！

ま，いまのとこ, Cを小さくすれば大丈夫：

...
int main(){
  std::filesystem::path myPath=getenv("HOME");
  myPath/="Data/test03";#ifdef USE_JACOBI
#ifdef USE_JACOBI
   Jacobi JJ;
   JJ.C=0.2;　　　　　← Cを結構小さくしている
   JJ.resize(200);
   JJ.Init();
   JJ.Solve();
   JJ.Save(myPath/"C02_N200.jac");
   JJ.Inv();        //逆行列で
   JJ.Save(myPath/"C02_N200.sol");     //こっちが正解
#else
   ...

すると,

Jacobi solver initialized.
Iteration 1000: Error = 0.00211763
Iteration 2000: Error = 0.00126218
Iteration 3000: Error = 0.000933486
Iteration 4000: Error = 0.000753576
Iteration 5000: Error = 0.000636365
Iteration 6000: Error = 0.000550397
Iteration 7000: Error = 0.000481946
Iteration 8000: Error = 0.000424612
Iteration 9000: Error = 0.000375222
Iteration 10000: Error = 0.000332059
Timeout. Error= 0.000332059
Saved: "/Users/sugimoto/Data/test03/C02_N200.jac"
Saved: "/Users/sugimoto/Data/test03/C02_N200.sol"
The program '/Users/sugimoto/test/PROG_EXE/P4/main' has exited with code 0 (0x00000000).

できたのかな？Jacobi解と逆行列解を比較してみた:

arm64:~ $ cd Data/test03/
arm64:test03 $ graph -Tps -C -m 1 C02_N200.jac -m 3 C02_N200.sol |ps2pdf -dEPSCrop - new.pdf
arm64:test03 $ open new.pdf

こんな感じ：

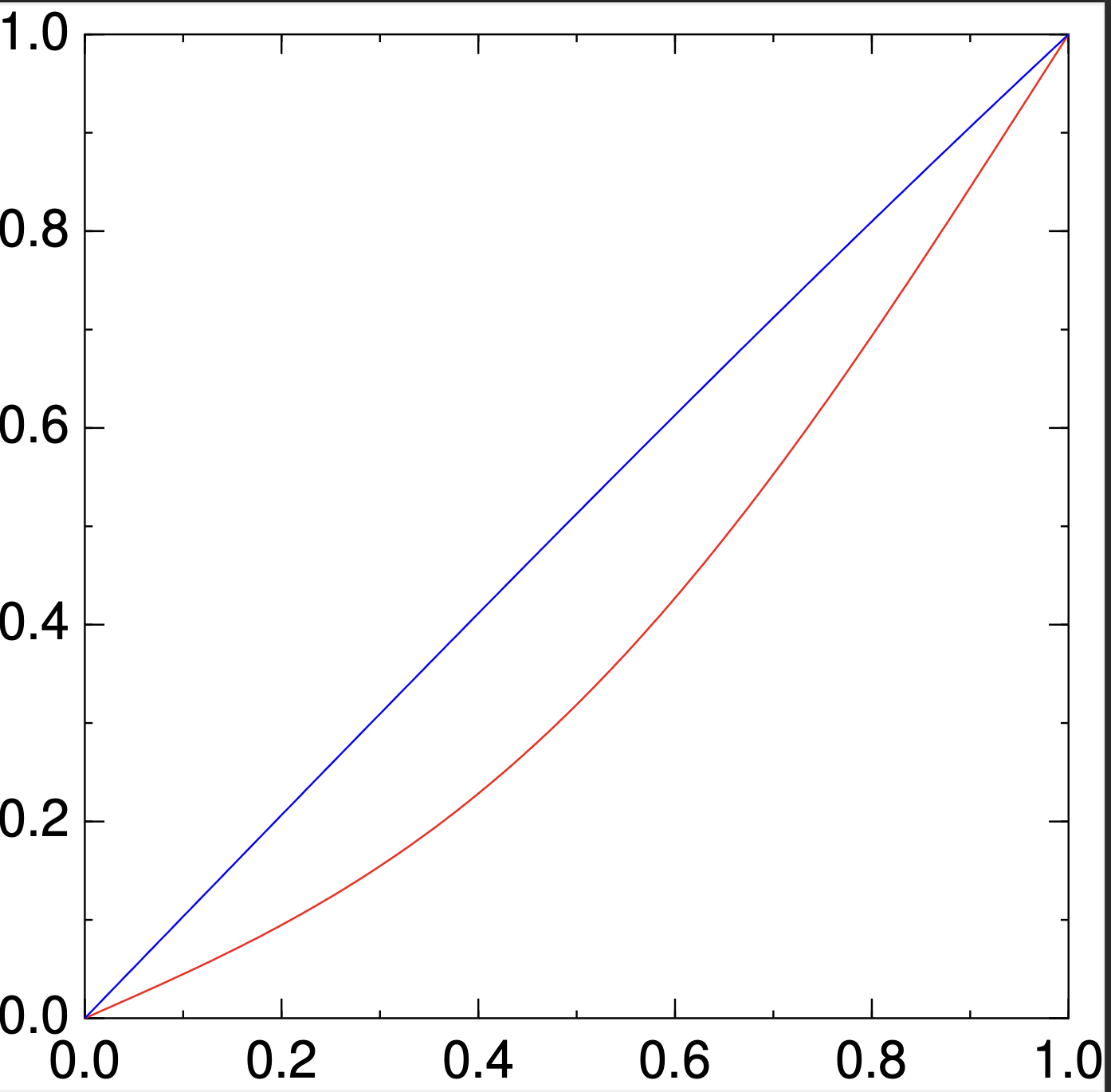　赤がJacobi, 青が逆行列

違うやん？とおもって実行結果をよくみると「Timeout. Error= 0.000332059」と出ていて，収束しなかったことがわかる．じゃ，

繰り返し回数が，もっと必要
で，何回まで必要なのか？は，ある程度回数ごとに出力してみて, 良さげな感じになるのを待つ必要がある．

配列ではない，何かへ

そこで，「指定した回数の時にプロファイルを書き出して欲しい」という願いが生まれます．一つ目の方法は,

if (!(iter%save_iter)) 書き出すんじゃ;

とプログラムして, 保存します．まあ一番簡単でよろしいのですが，

1000回に1回保存でいいかな，とおもって3ヶ月前に始めたんだが，10000000回やったが，まだである．
1000回おきの保存が無意味になってきた・・・

という経験が，結構たくさんあります．そこで，「指定した回数において，書き出せ」を行う方法を覚えましょう．

こういう，あまり機械的ではないデータを保存するために, C++には，たくさんの「配列ではない，何か」が用意されています．総称して「コンテナ」と呼びます．いくつか紹介しましょう:

集合コンテナ

読んで字の如く, 何かが集まった「集合」です．

#include <unordered_set>
...
std::unordered_set<size_t> SaveTimes;
SaveTimes.insert(1000);
SaveTimes.insert(2000);
SaveTimes.insert(5000);
SaveTimes.insert(10000);
std::cout << "SaveTimes= ";
for(auto &T:SaveTimes) std::cout << T;
std::cout << std::endl;
std:cout << "2000 はあるかにゃ? " << SaveTimes.contains(2000) << std::endl;// 1 が得られる
std:cout << "2001 はあるかにゃ? " << SaveTimes.contains(2001) << std::endl;// 0 が得られる

ここは集合の中身を画面に出す. こういうコンテナ系では，範囲指定for文が便利ですね！さて，出力は， SaveTimes= 10000 1000 5000 2000 などになります．え？大きい順？入れた順でもない．unordered_set は, 順序には全く無関心で，高速という点に全振りした「集合」なのです. こういった，探し出すとかの関数が高速なのです．他にどんな関数が使えるのかは, AIモンキーに聞いた方が早いです．

それは嫌だ，小さい順とか大きい順とか，面白い順とかで並び替えて欲しい場合，std::set を利用してください．ただし, 整数とかなら小さい順は明確ですが，「面白い順」など，定義不明瞭な順序である場合，あなたが, ここで学習する「オペレータ」を用いて順序を定義する必要があります．

MAPコンテナ

集合に，キーワードがついたものです．つまり(key, value)の集合のセットです. キーワードを与えると値がわかるので, 数学的には「写像」ですね！

#include <map>

#include <string>
...
std::unordered_map<std::string, int> FaceList;
FaceList["Sugimoto"] = 1002053;
FaceList["Kawasaki"] = 2002022;
FaceList["Sugimoto"] = 3000000;
FaceList["Tako"] = 8;
for (auto &[key, value]:FaceList) std::cout << key << " : " << value << std::endl;

ここが(key,value)それぞれの変数タイプを指定する場所です．この例では，keyはstd::string文字列, valueは整数です．std::stringは新顔ですが，これは"Sugimoto"などの「文字列」です．よく使われるものなので，大体の局面で使えますが，正しくは #include <string> してから利用します．mapの特徴は, FaceList["キーワード"] のようにキーワードを指定すると，その要素が存在しなければ作成される．つまり，「存在するのかな」とおもってFaceList["キーワード"]すると, 項目が作成されてしまうということです．さらに, このように, 同じキーワードで値を指定すると，最後のやつが有効になります. いやそれは困る，同じキーワードで複数の値を入れたい場合には, std::multimapを利用してください．で, unordered_mapも, キーワードの順番に興味がないです（その代わり，高速である）. キーワードを何らかの基準で並び替えて欲しい場合, std::map を利用してください．これは範囲指定for文の書き方です. &[key,value] と書かなければいけないことに注意．

他にもListコンテナが有名ですが，それは後ほど．

実行してみるの逆襲

では，設定したSaveTimesおきに, ファイルを作成したら，収束の具合が分かりそうですね．そこでJacobiクラスを変更:

...
#include <unordered_set>
...
class Jacobi
{
   ...
public:
   std::unordered_set<size_t> SaveTimes;
   std::filesystem::path filename;
   ...
   Jacobi()
   {
      SaveTimes.clear();             //お行儀よく，SaveTimesは初動で空っぽにしておく
      filename="FuckingTaco.data";   //ユーザーによってはfilenameを与え忘れるであろう．そんなお馬鹿さんにプレゼント
   }
   ...
   bool Solve(size_t max_iter = 10000)
   {
       std::filesystem::create_directories(filename.parent_path());
       std::ofstream ofs(filename);
       ...
       while (iter < max_iter)
       {
           ....
          //if (!(iter%message_iter)) ....
          if (SaveTimes.contains(iter))
          {
              std::cout<< "Saveing to [" << filemame.string() << std::endl;
              ofs << std::endl << "# iter = " << iter << std::endl;
              ofs << 0 * dx << " " << Y0 << std::endl;
              for(size_t i=0;i<x_new.size();++i) ofs << (i+1)*dx << " " << x_new[i] << std::endl; 
              ofs << x_new.size() * dx << " " << Y1 << std::endl;
          }
       }
       ...
       return iter != max_iter;
    }

これは途中経過を保存するファイル名で, Solve()開始直後に作成してますね！で，ここら辺で, 保存するべき回数かどうかをチェックしてます. 保存すべきであれば, ここいらへんで出力してますが，そこで疑問：ここいらへん，何してるんだろ

これはPlotUtilsソフトの癖(仕様)で

空行があったら，次の曲線を描く．色とか点線を切り替えて，区別できるようになる. なので，最初に空行を入れるために std::endl をぶちかます
#で始まる行については，メモ書きをつけてOK. なので # iter = 1000 とか，わかるようなメモを書き込んでおる．

さらに，Solve()がbool=true/false を返却するようになってます．この辺で，返却してますね．先程は，収束してないのに「警告！！！収束せんかったし！！！」とか，エラーを出さなかったので気づかなかったんですよね．

では, main()の方は

...
   Jacobi JJ;
   JJ.C=0.2;　　　　　← Cを結構小さくしている
   JJ.resize(200);
   JJ.Init();
　　JJ.filename=myPath/"C02_N200.data");
   JJ.SaveTimes.insert(10000);
   JJ.SaveTimes.insert(20000);
   ....

   if (!JJ.Solve(1000000)) std::cout << "ERROR!! OOPS!! DID NOT CONVERGE FUCK" << std::endl;
   JJ.Save();
   JJ.Inv();        //逆行列で
   JJ.Save(myPath/"C02_N200.sol");     //こっちが正解
#else

これなら，失敗してたら気づくであろうよ.

Jacobi solver initialized.
Iteration 1000: Error = 0.00211763 Save to [/Users/sugimoto/Data/test03/C02_N200.dat]
Iteration 2000: Error = 0.00126218 Save to [/Users/sugimoto/Data/test03/C02_N200.dat]
Iteration 5000: Error = 0.000636365 Save to [/Users/sugimoto/Data/test03/C02_N200.dat]
Iteration 10000: Error = 0.000332059 Save to [/Users/sugimoto/Data/test03/C02_N200.dat]
Timeout. Error= 0.000332059
ERROR!! OOPS!! DID NOT CONVERGE!!

おお, これなら，失敗したことが明確に伝わるので，よろしい！

で，失敗していることについても対策しましょう．

Jacobi法は遅い．数学を学び，Gauss-Sidelの方がマシであることを学んだので，方法を改める
Jacobi法は遅い．数学を学び，有限回数で収束することが保障されている共役勾配法で攻める．
数学を学び, エイトケン加速とかでパワーアップ！
学ぶのは面倒なので，繰り返し数を増やし，力押しする．
学ぶのは面倒なので，収束限界 tol=1e-10 を 1e-4 にし，妥協する
ここを学んで計算機に早く計算していただく

ここでは, 4番, 5番でやってみましょう！

Jacobi solver initialized.
Iteration 1000: Error = 0.00211763 Save to [/Users/sugimoto/Data/test03/C02_N200.dat]   ←途中経過ファイル
Iteration 2000: Error = 0.00126218 Save to [/Users/sugimoto/Data/test03/C02_N200.dat]
Iteration 5000: Error = 0.000636365 Save to [/Users/sugimoto/Data/test03/C02_N200.dat]
Iteration 10000: Error = 0.000332059 Save to [/Users/sugimoto/Data/test03/C02_N200.dat]
Converged in 19919 iterations.
Saved: "/Users/sugimoto/Data/test03/C02_N200.jac"   ←Jacobi最終ファイル
Saved: "/Users/sugimoto/Data/test03/C02_N200.sol"　 ← 逆行列ファイル（正解）

できたぞ！グラフ描いてみよう．逆行列で求めた正解ファイルを赤線で, Jacobi法の結果を緑で，途中経過をそれ以外で書いてみる:

arm64:~ $ cd Data/test03/
arm64:~ $ graph -Tps -C -m 1 C02_N200.sol -m 2 C02_N200.jac -m 3 C02_N200.dat |ps2pdf -dEPSCrop - new.pdf

で，結果はこちら：

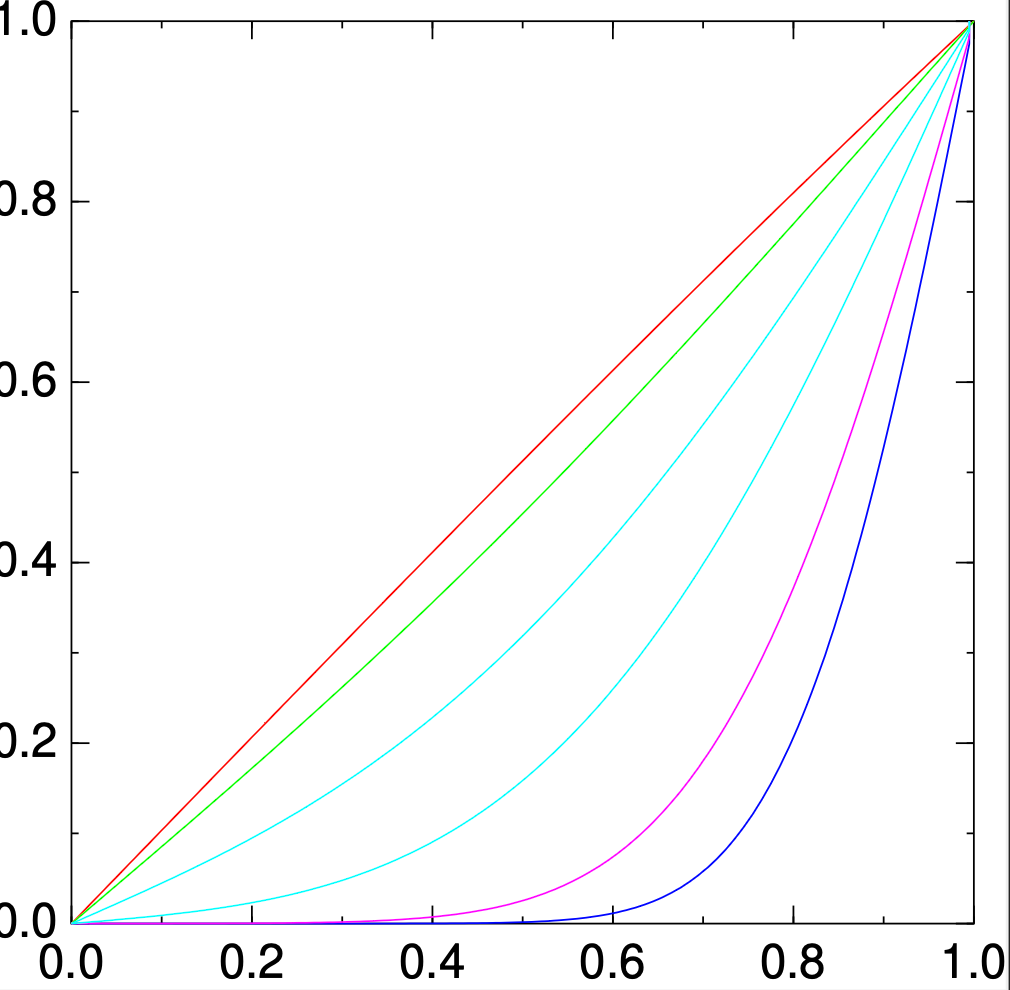
たしか, 「誤差」tol=1e-4 に設定した．だが，赤線と緑線の差は，0.01以上はありそうである．

そりゃあんた, tol でチェックしてるのは，x_old と x_new の差である．1e-4 のズレを1万回続いたら 1 ズレるやん．
- 当然ながら, 1e-10のズレが\(10^{10}\)回続いても, 1ずれるマスよ〜
x_old と x_new の差なんて, 誤差でも何でもないです．
じゃあどうすんねん！それは，ここで学びましょう．

というわけで，ここでは敗北決定，撤退しましょう．

添付	サイズ
SrcFiles.zip	358.76 KB
SrcFiles_0.zip	1.11 MB

常微分方程式III