メインコンテンツに移動

数値積分

数値積分

数値積分とは，コンピュータで\(\displaystyle\int_a^b f(x)\mathrm{d}x\)を計算することです．で，まあ状況は2通りあって

  • 状況A \(f(x)\)は，何か別の数値計算で得られる．なので，例えば\(x_i=i\Delta\)のような「格子点」上の値しかわからねえ．だが, その点の上のデータはit’s freeで, 初めからわかっておる
  • 状況B \(f(x)\)の形はわかっておるので，なんぼでも計算できるが，1点計算するのに1万円かかる

という感じですね．まずは最初に，両方で使える手法を学び，次に，プログラムの書き方が少々特殊で，「xの数値ではなく，関数を与える」必要がある後者を学びましょう．

オイラは自作派

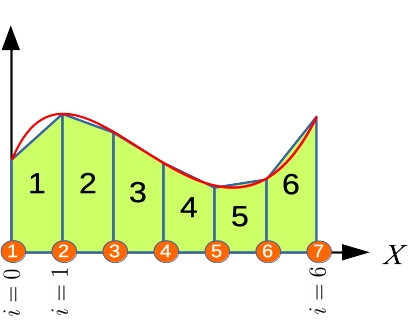
数値積分を自作する手もあります．台形則なんて素晴らしいですよね. これは状況A状況B どちらでも使えます． ええっとこれは，確か台形の面積が上辺＋下辺かける高さ割る2，だったので，区間\([a b]\)を\(N\)等分して\[\int_a^b f(x)\text{d}x=\sum_{i=0}^{N-1} \frac{f(x_{i})+f(x_{i+1})}{2}\Delta x\]ってわけですよね．

figs

問題例1

とりあえず簡単な定積分を行ってみる:

\[ e^{-U^{2}}+\frac{1}{2\sqrt{\pi}}\int_{0}^{2\pi}\exp\left[-U^{2}\sin^{2}\theta\right]\text{erf}\left(U\cos\theta\right)U\cos\theta\text{d}\theta=1 \]なんてどうでしょう. なお\[\text{erf}(x)=\frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}\text{d}t\]でしたね．いくらなんでもちょろいですね．まあこんな感じか. まず被積分関数を定義して

double integrand(double th,double U)
{
  auto UC=U*std::cos(th);// auto でもdoubleでも大差ないな
  auto US=U*std::sin(th);// std:: は省略しても同じ
  auto ERF=std::erf(UC); // 誤差関数は標準関数です
  auto EXP=std::exp(-US*US);
  auto COEF=M_2_SQRTPI/4.;  //【Jump to Definition】すれば定義がわかる
  return COEF*EXP*ERF*UC;
}

んで，足し合わせるだけですね：

double sum=0.;
for(int i=0;i<N;i++)
{
  double y0=integrand(dth*i,U);  //細かく言えばy0は前回のy1なので手抜きできる
  double y1=integrand(dth*(i+1),U);
  sum+=dth/2*(y0+y1);
}
sum+=std::exp(-U*U)-1.;

結果を見てみると, \(U=1\)ならばこんな感じ:

\(N\) 10 20 40 80
誤差 \(4.2\times10^{-5}\) \(1.9\times10^{-12}\) \(-2.2\times10^{-16}\) \(-1.1\times10^{-16}\)

最初は調子良く誤差が減るのに, 最後はあまり変わりません．double 浮動小数点数は，およそ15桁しか有効数字がないので，\(10^{-12}\)レベルから先は計算が怪しげになるからです.

台形則でも十分ですが，シンプソン公式を用いると，もっと良いです. プログラムしてみましょう．

問題例2

先程敗退したJacobi法ですが, まずは「ほれほれ，こんなに収束遅いっすよ」という内容を，数値積分を使って表現してみましょう．具体的には繰り返し数\(n\)の状態を\(y_n(x)\)として, \[S_n^2=\int_0^1 |y_n(x)|^2 \mathrm{dx}\]とでも定義し, \(S_n\)が, どのように変化しているのかを調べましょう．

せっかく作成したプログラムですので，この状況をCommitしていたとします:

GITブランチの作成

このプログラムを改造していくのですが，元の状態とは異なったものになるし，オリジナルの状態も保存しておきたいです．そういう時には，枝をつけます！ブランチ，と言います．

【ブランチの作成】で，何か区別できる名前をつけます:

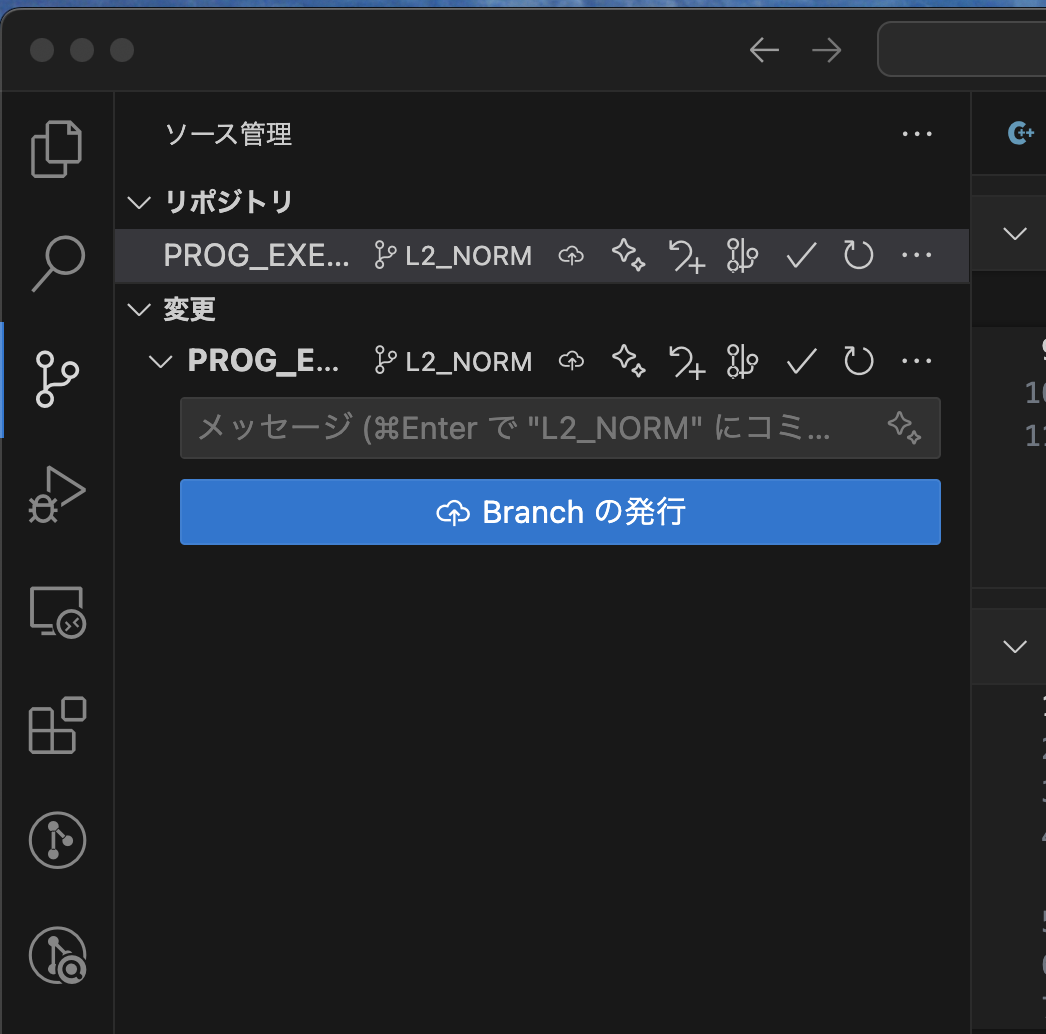　発行！

GITブランチ間を移動

作成したブランチは，どっちを編集するか，移動できます．試してみましょう．

今はL2_NORMにいるので，何か変更してCommitしてみてください．で，オリジナルの main ブランチに戻ってみる：

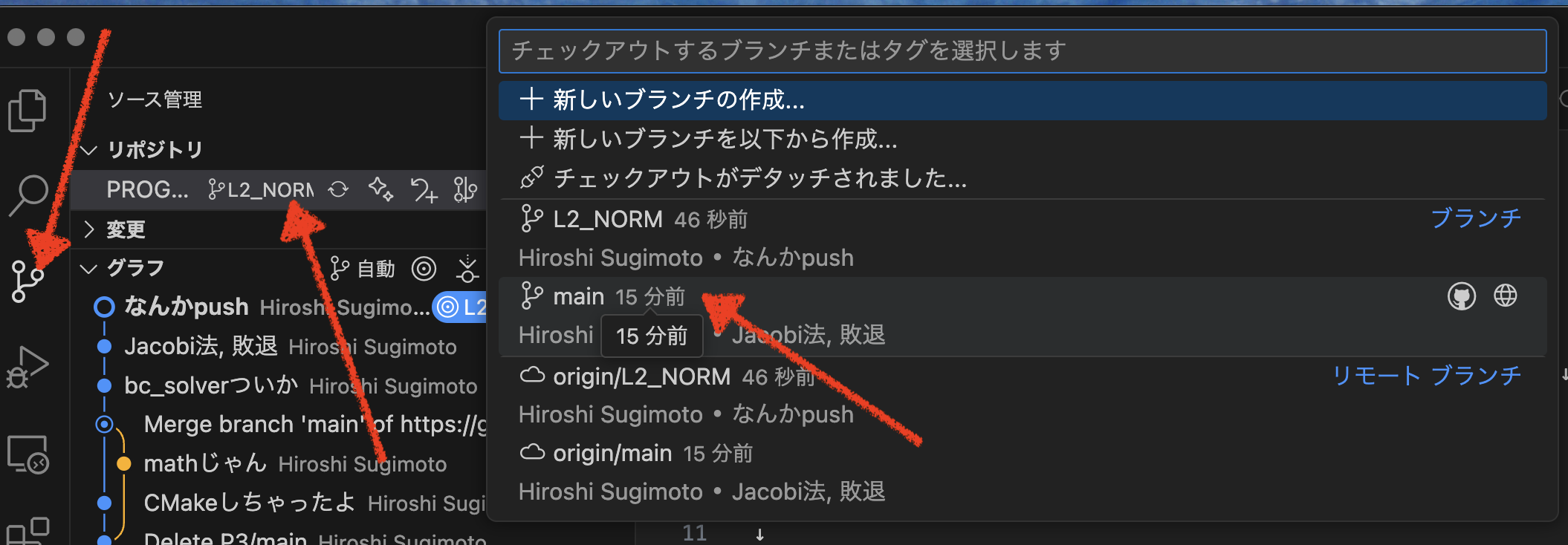
すると，編集したのが消えて，元に戻っているはずです．そこで，何か変更してCommitしてくださいね．

で，どういう状態になったのか，全体を見てみよう.

  

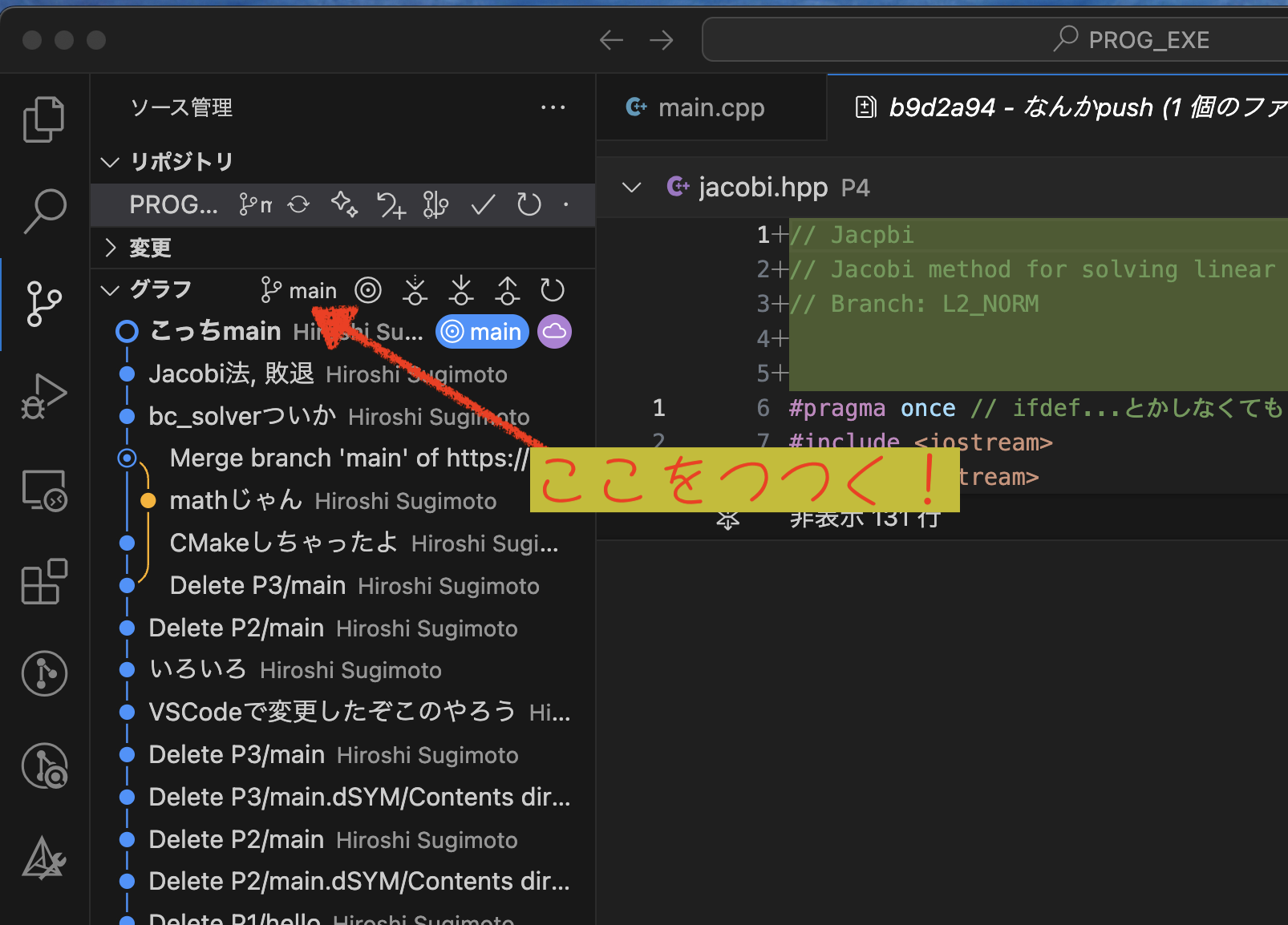
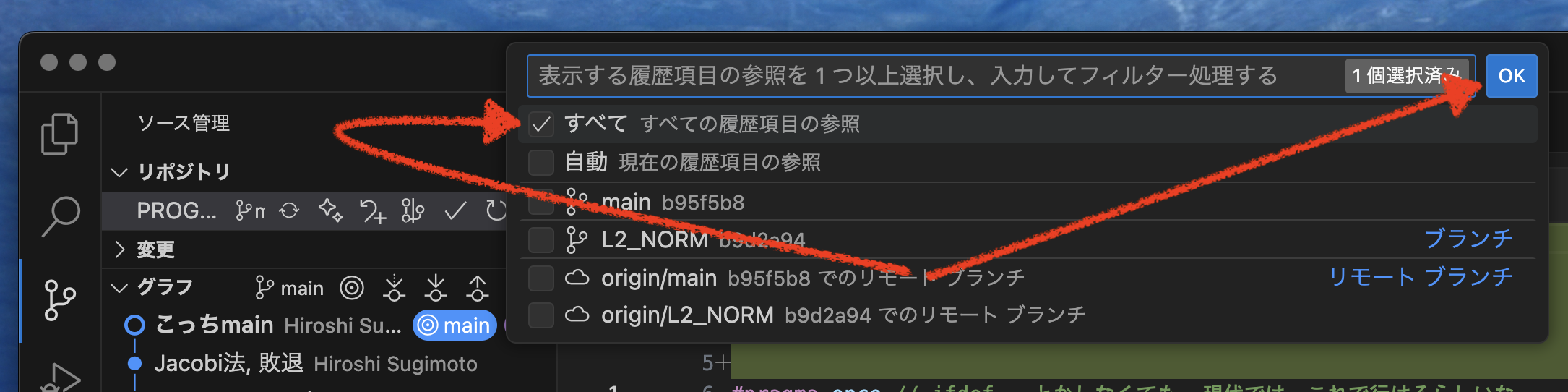
すると

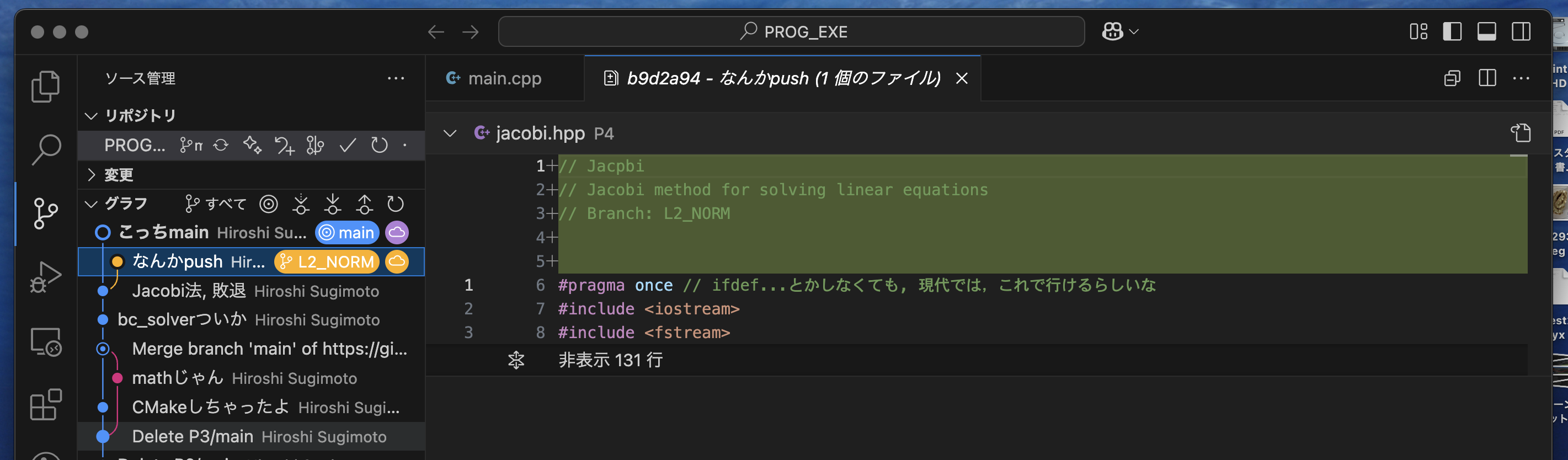
  • mainブランチと, L2_NORMブランチがあることがわかる
  • それぞれのCommitをクリックすると，そこでどのような操作が行われたかをみることができる！
  • で，現在いるブランチは◎がついているので，現在は main ブランチにいることがわかる

解析結果の離散データを積分

では, 先程敗退したJacobi法で改造を進めましょう．

#include <iomanip>
class Jacobi
{...
    std::filesystem::path filename;
    std::filesystem::path logname;   // 記録を残すファイルを指定
    ...
    bool Solve(std::filesystem::path logname="")
    {
       size_t max_iter = 0; // いやあ．最大繰り返し数指定するの面倒になったんで
       for(auto &n:SaveTimes) max_iter=std::max(max_iter, n);//保存指定回数の最大値が，最大繰り返し数で，ええやん
 　　　 std::ofstream lout;     // 記録を取るファイル．下で見えるように，ここで定義
       if (!logname.empty())   // logname が指定されていれば記録を取る
       {
           std::filesystem::create_directories(logname.parent_path());
           lout.open(logname);
       }
       // 解析実行
       while (iter < max_iter)
       {
          ...
            // x_new の積分を求める
           if (lout)   // 記録を取る場合
           {
               double sum=0.0,x_pre=Y0;
               for(auto& v:x_new) sum+=(x_pre*x_pre+v*v)*dx*0.5, x_pre=v;
               sum+=(x_pre+Y1*Y1)*dx*0.5;
               lout << iter << " " << std::setprecision(15) << std::sqrt(sum) << std::endl;
           }

この辺が数値積分．で，この辺でファイルに記録を残しています．Solve()では記録を取らないが, Solve(ファイル名)だと記録を取る，ということです．これは，記録を取るようにファイルを開いていたら，を意味しています．ここは完全な新顔ですが，これは，読んでわかるように，15桁の精度でファイルに書き出しています． これで採取した\(S_n\)の様子は，以下の通り：

　

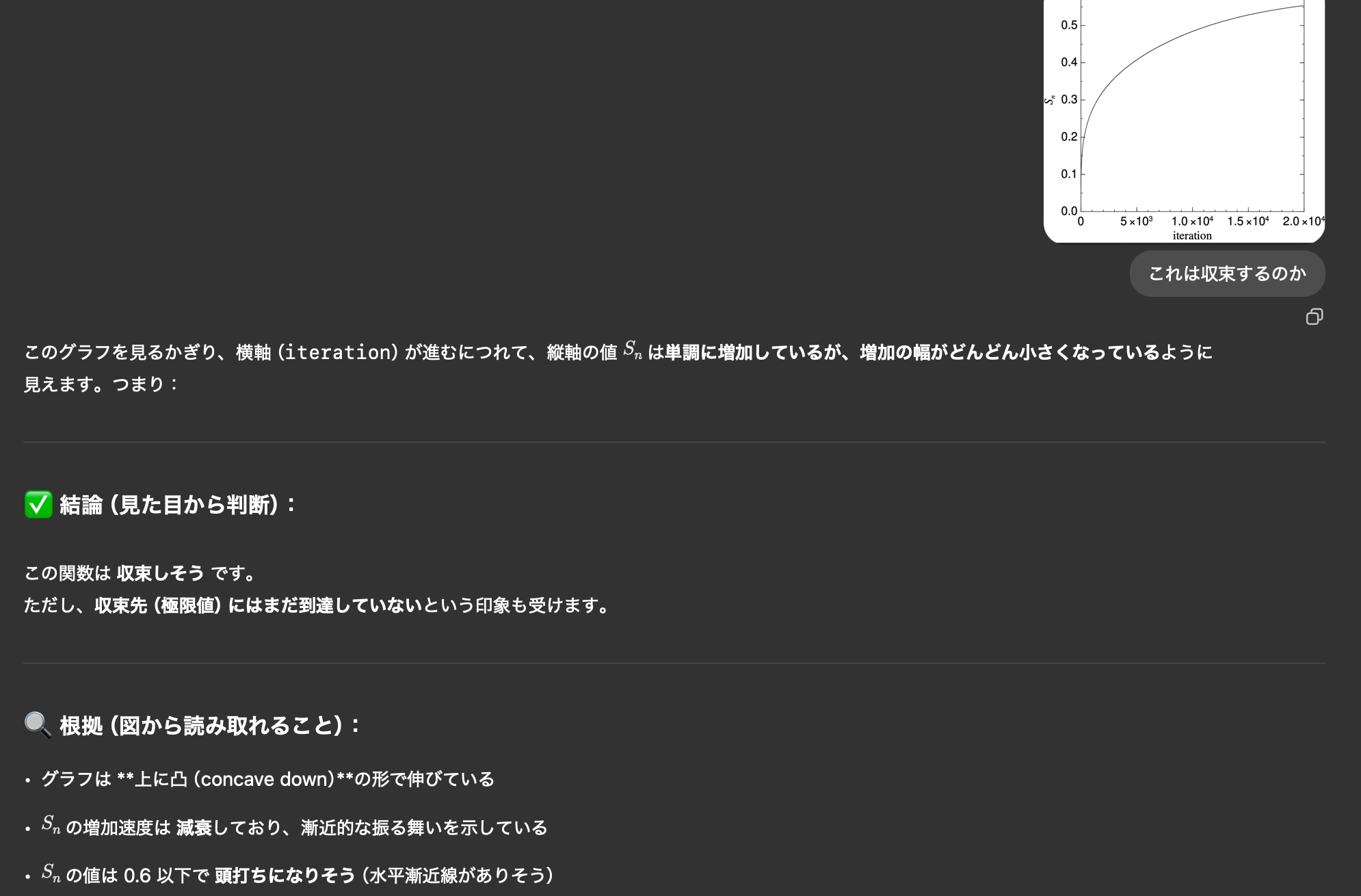
座標軸が少々かっこよくなってますが，これは

arm64 $ graph -Tps --label-font-name="Times-Italic" -Y "S\sbn\eb" -X "\fRiteration" C02_N200.log |ps2pdf -dEPSCrop - new.pdf

こう書いているだけです．さて，この図を見て，いろいろな感想を持つ人がいます：

  • こいつは，そのうち, 0.8程度で一定になる
  • こいつは，そのうち, 0.6程度で一定になる
  • こいつは, 一定値に収束せず, n → ♾️ で発散する．

どれが本当なのでしょうか？　（学生さんの中には，こりゃあ運が悪いケースだ，と思っている人がいるかもしれません．そんなこた，ないですよ．研究なんて，いつも，これっす！私は学部4回生でこれと戦うのに半年かかりましたよ）chat-GPTは「収束するに100円」的な感じですけどね．

こういうのは，微係数とか毎回の変動を対数グラフで書いてみるとわかるんですよ．

arm64 $ gawk '{if ($1>1) printf("%d %.15f\n",$1,$2-y);y=$2}' < C02_N200.log  > C02_N200.diff

これはgawkという，タイプライターExcelソフトです(MacOSでは，何もインストールしなくても，類似の awk というのが標準でついている．ほとんど同じものである)．$1は1コラムめ，$2は2コラムめで，数式を書いたらExcelマクロみたいにここを毎行計算します．途中のこの辺は，ふる〜い形式の画面出力の書き方です：

  • printf("書式名", データ, データ,....)   で, %fだと7桁実数，%.15fだと15桁実数, %dだと整数・・・\nは std::endl のこと

です. で. 1行づつ，2コラムめをyとして保存． 毎行出力するのは1コラムめと, 2コラムめのyからのズレ(つまり上の行からの変動値)になります．これは，C02_N200.logファイルから読み込め，ってことで，これは，C02_N200.diff というファイルに書き出せ，ということです．「ご苦労様　＞　おかあちゃん　< こどもたち」（こどもたちが，おかあちゃんに「ご苦労さん」と述べている）みたいなノリです．

これを図に描くと

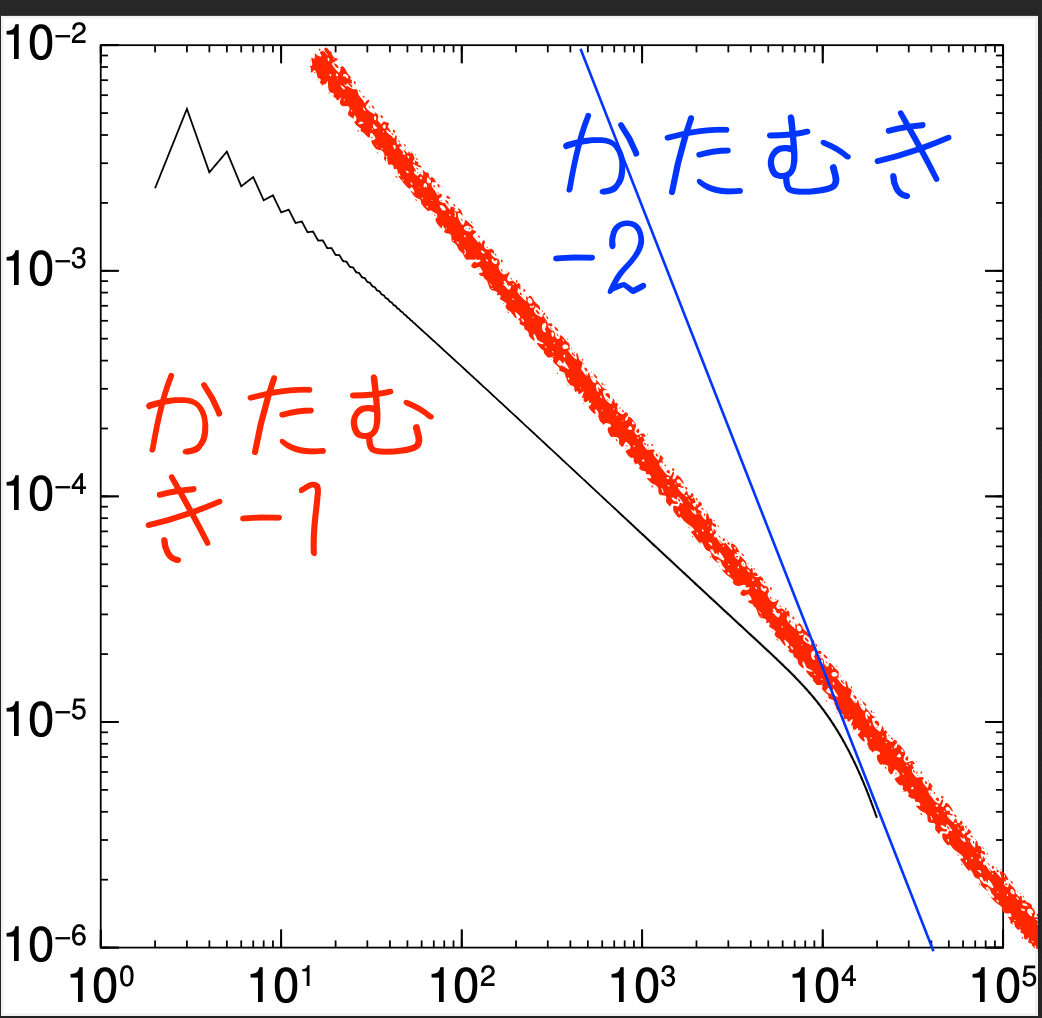
両軸とも対数グラフです．ええっと graph -Tps -lx -ly C02_N200.diff です．で，最初のころは傾きが-1よりデカく，n=10000 あたりで傾きが-2って感じですね．すると

\[   \log (S_n -S_{n-1}) < -2 \log n + \mathrm{Const}\] つまり\[   S_n -S_{n-1} < Cn^{-2}\]であるので, \[   S_\infty -S_N < \sum_{n=N}^\infty \dfrac{C}{n^2}<\infty\]であるから，こいつあ，収束するんですね！さらに, 最後の\(S_N-S_{N-1}=E\)がわかってれば, \(C=EN^2\)であるので，そこからのズレが, せいぜい，\[\sum_{n=N}^\infty \left(\dfrac{N}{n}\right)^2 E \sim  \int_1^\infty \dfrac{1}{x^2}\mathrm{d}x  NE\sim NE\]であることもわかります．ええっと, 最後\(N\sim 20000\)ズレが\(3\times 10^{-6}\)だから，あと\(S_n\)は0.06くらいアップするんですね．誤差が0.00001に到達するには，くり返し数はN=100000000程度が必要なこともわかる．

こういう計算は必要ですよ．やっぱ，卒業する前に計算は終わった方がベター

ただしこれは傾きが-2以下になった場合であって, 傾きが-1よりも大きい n = 15000 のころまでは，「発散するように見える」と述べるのがただしい. 収束するように見えるのは, n > 15000になってからに限る，のが正しいのだ．いや〜人間の目には，n=15000で，そんな違いが現れているようには見えない．やっぱ検証するって大切ですよね．

与えられた関数を積分

今度は, 与えられた関数\(f(x)\)を, 与えられた範囲\(a<x<b\)で積分してみましょう. 練習のため, mainブランチから, 何か新しいブランチ「問題3」を分岐して，そこで作成してみましょう．

さて, いままでの変数とは, x とか filename とか，値を持つものでした．C++では，変数として「関数」を与えることができます．こんな感じです:

// IntFunc.hpp: 与えられた関数を積分
#pragma once
#include <iostream>
class IntFunc
{
public:
   IntFunc(){};
   double Get(std::function<double(double)> F, double x)
   {
       return F(x);
   }
};

これが，関数を表す変数型です．みた感じでわかると思いますが, これは実数から実数への関数\(f(x)\):\[x\in \mathbb{R}\to f(x) \in \mathbb{R}\]を表してます．で, Get(F,x)で, F(x)の値を戻すはず．やってみましょう.

// main.cpp
#include <iostream>
#include <cmath>
#include "IntFunc.hpp"
int main() {
   IntFunc OBJ;
   std::cout << OBJ.Get([](double x) { return std::sin(x); }, 0.5) << std::endl; //途中まで入力したら，AIモンキーがこれを書いた
   return 0;
}

AIが書いたGet()のこの辺がさっぱりなので解説します．これはラムダ式というものです．

ラムダ式

ラムダ式とは, 名前がなく, 名前で呼び出すことが不可能な関数です．名前はありませんが，「あれやって，これやって，・・・」という手順はあるわけです．そこで，それを変数に入れると，呼び出せるようになります．なにぶん「手順」という値ですので，

  • 他の関数の引数に入れられる
  • コピーしたり，関数の値として呼び出し元に返したり

まるで数値のように関数が使えるわけです．ラムダ式の定義は簡単で

auto F=[](){std::out<<"はろー" << std::endl;};

最初の[]がラムダ関数の開始命令, 関数の引数がこれ, return文がなければvoid型ってわけです．値を返却する場合は, return文を入れると, まあ推定してくれます:

auto F=[](int j){std::out<<"はろー" << std::endl;return j+1;};

この例ですと, jが整数 int ってこた j+1も普通 int なので, たぶん，Fの値は int になります．「たぶん」が嫌なら, 

auto F=[](int j)->auto{std::out<<"はろー" << std::endl;return j+1;};

あれ？これでは auto 推定なので多分のままだわ. じゃ， 

auto F=[](int j)->int{std::out<<"はろー" << std::endl;return j+1;};

これなら，疑いの余地なく int ですね!    最初の[]に微妙に疑問を覚える人は，ここをみてね♡

これらを受け取った変数Fは，数値ではなく，手順を覚えています．どう使うのかといえば, 

auto ret=F(); //retには戻り値のコピーが代入される

これで呼び出すことができます．FをPoiPoiという変数にコピーしたら，同じ関数の呼び出しが 

auto R2=PoiPoi() ;

になります（手順をコピーしたので！）．なんといっても変数ですから，他の関数の引数に与えることができます. 

OBJ.Get(PoiPoi,....);
あるいは
OBJ.Get([](){std::out<<"はろー" << std::endl;return 0;},...);

1行目はまあわかりますね．2行目は，もう面倒くさいので引数の値としてラムダ式を書いています．AIが書いたのは，これですね！

じゃ，OBJ.Get(std::sin,0.5)でも良いのか？というと，オーバーロードされているので無理です．回避方法はAIモンキーが教えてくれますが，まあ，ええわ

というわけで, 数値積分コードを追加してみょう. IntFuncクラスにIntegrate()関数を作ろうとすると, AIが書いてくれました：

         ...
        return F(x);
     }
    double Integrate(std::function<double(double)> f, double a, double b, double eps = 1e-6) const {
       double sum = 0.0;
       int n = 100; // 初期分割数
       double h = (b - a) / n;
       while (true) {
           double new_sum = 0.0;
           for (int i = 0; i < n; ++i) {
               new_sum += f(a + i * h + h / 2.0); // 中点法
           }
           new_sum *= h;
           std::cout << "n= " << n << ", sum= " << new_sum << std::endl; // デバッグ用出力
           if (std::fabs(new_sum - sum) < eps) {
               return new_sum; // 精度が満たされたら終了
           }
           sum = new_sum;
           n *= 2; // 分割数を倍にして再計算
            if (n>1000000000) // もし分割数が大きすぎる場合は終了
               throw std::runtime_error("Too many iterations, 
　　　　　　　　　　　　consider increasing the initial n or decreasing eps.");
           h = (b - a) / n;
       }
   }

うん．シンプルなプログラムで新規の文法要素はないすね！ここいらへんは，ちょっと心配なんで足してみました(心配になって if と入力したら, あとはAIモンキーが勝手に心配した)．ではやってみる! :\[\int_0^{1} \frac{1}{\sqrt{x(1-x)}} \text{d}x=\pi\]とかどうですかね．

 int main() {
   IntFunc OBJ;
   std::cout << OBJ.Integrate([](double x) {
           return 1.0/std::sqrt(x*(1.0-x));   //ラムダ式の途中で改行とか，好きにしてね
       }, 0.0, 1.0) << std::endl;             //C++は, { と　} しか，見てないんで〜
   return 0;
}

で，やってみると

．．．
n= 6553600, sum= 3.14112
n= 13107200, sum= 3.14126
n= 26214400, sum= 3.14136
n= 52428800, sum= 3.14143
n= 104857600, sum= 3.14147
n= 209715200, sum= 3.14151
n= 419430400, sum= 3.14153
n= 838860800, sum= 3.14155   ええっと π=3.14159265358979だったよね
libc++abi: terminating due to uncaught exception of type std::runtime_error: Too many iterations, consider increasing the initial n or decreasing eps.

怒られちゃった？！　1000000000分割しても誤差が大きいみたい. 天文学的な分割数をしているのに，精度は全然ダメですねえ・・・

この関数は, \(x\to 0, x\to 1\)で\(y\to\infty\)になってるんで, 普通に等分割してたらダメです．変数変換したらもっと簡単になるのはもちろんですが，実戦では，「実は被積分関数は数値データなので，式が不明である．端点で発散することは知っている」「被積分関数の1点を計算するのに千円かかる．なお予算は5万円である(じゃ，今回の経費は8000億円ですね)」「変数変換はグルに禁止されている」ということが多々発生するわけです.仕方ないですね．\(x\in[\epsilon,1/2]\)の積分で誤魔化すことにしましょう.．．．といって工夫し始めると，どんどん時間がかかっていきます．

オイラは他力本願

めんどくさくなってきたので，プロが書いたライブラリーに積分してもらいましょう．まず，添付の intde.hpp をフォルダーに追加してください．これは，数理研の森先生が作った多重指数変換自動積分プログラムです．とりあえず使ってみる！

...
#include <iomanip>
#include "intde.hpp"
int main() {
   IntDE myIntegrator;
   size_t count=0;
   double err,err_req=1e-6;
   myIntegrator.Initialize(err_req); // 初期化
   auto v=myIntegrator.Integrate([&count](double x, void *param) {
       count++;
       return 1.0 / std::sqrt(x * (1.0 - x)); 
   }, 0.0, 1.0, err);
   std::cout << "Integral value: " << std::setprecision(12) << v << ", Error: " << err
　　　 << " requested: " << err_req << " by " << count << " steps"<< std::endl;
   return 0;
}

とりあえずここで，IntDEクラスを読み込みます．で，インスタンス作成は普通通り．仕様により，まず初期化を行わねばなりません．引数で与えているのは，あなたが希望する積分精度です．呼び出し方法は，自作のものと大して変わらないですね．でもまあ，こことか，ここは何してんだ？ですがまあ，あとで説明しますね！なお，ここは，実現した計算精度が返ってきますので，何か倍精度の変数を入れておいてください．なお，ここいらへんは，書き出す数値の桁数を12桁にする方法です．じゃ，動かしてみるか・・・

Integral value: 3.14159260183, Error: 6.27986490903e-06 requested: 1e-06 by 25 steps

・・・なんじゃこりゃ．25回しか関数を呼び出してないので，ご予算は3万円以下で，僕らの8000億円とは桁違いです．精度の推定値は\(6\times10^{-6}\)で，結果が  3.1415926018 なので，実際の精度は \(5\times10^{-8}\)

化け物ですね．プロの仕事とは，このようなものです．決して，勝負を仕掛けてはなりません．

数値積分を自分でコード書いている人は，間違いなくNoobですので，撃破可能です. 税金の無駄遣いを発見した，といって国税庁に告発するのもアリです．

で，意味不明なコードがあるので，解説していきましょう．

void *ってなに

これは，ポインターを勉強しましょう．

ポインター

ポインターとは，変数の値を記録している場所のことです．コンピュータでは，変数の値をメモリー

ddr4

に保存しています．これは，変数を記録しているところが一列に並んで，アドレスで区別しています．

addr

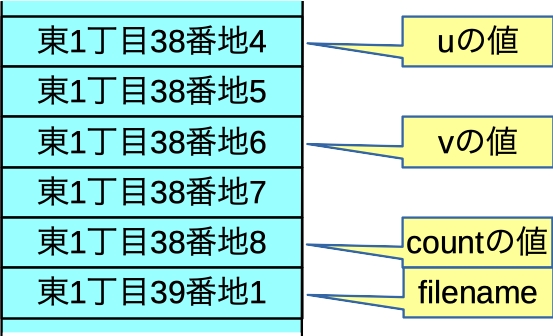
まあこんな感じですかね．で, プログラム中に count と書けば, 1 とか44とか，値がわかるわけですが，&count と書くと，アドレス「東京都葛飾区若松町東一丁目38-8」がわかるわけです. この，変数の「住所」を，変数の値とすることができます．例えばdouble値を持つ変数の「住所」であれば，これは

double*

と書きます．例えば double X 変数があったら,

double* X_point = & X;

で, X_pointにアドレスの値が代入されます．C++では空白は意味がないので, double* と書く人や, double *と書く人がいます．X_point はdouble変数が入っている方向を指差していることになりますが，では，その指の先に書いてある値は,

*X_point

で取得できます・・・この辺で，ほとんどの人の頭はこんがらがってきます．では，以下のプログラムは正しいでしょうか．

double X=3.0, Y=2.0;
double* X_point=&X;
Y=X_point;

だめですね．Yはdouble数値なのですが, X_pointは「数値がある方向」です．「方向」はdoubleの数値ではないので，Yには代入できません．

double X=3.0, Y=2.0;
double* X_point=&X;
Y=*X_point;

であれば, X_point方向に書いてある値はdoubleの値3.0ですので, Yの値が3.0に変わります．混乱していると思うので，もう一度例えると

  • あなたの住所が，東京都葛飾区若松町東一丁目38-8であったとする．
  • 東京都葛飾区若松町東一丁目38-8によって，あなたを特定できる. 東京都葛飾区若松町東一丁目38-8の方向に行くと，あなたがいるからである．
  • しかし，あなたは哺乳類クラスの派生型：人類クラスの一つのインスタンスであって，東京都葛飾区若松町東一丁目38-8という物質ではない

IntDEでは，関数にパラメータを渡すために，ポインターが利用されています．上の例では使ってないですが，

...
int main() {
   IntDE myIntegrator;
   size_t count=0;
   myIntegrator.parm=&count;
   double err,err_req=1e-6;

こうすることで, myIntegratorは，必要なパラメータが myIntegrator.parm 方向にあることがわかります．パラメータは一つとは限らず，例えばパラメータクラスのインスタンスかもしれません：

class Parameter {
   ....
public:
   size_t count;
   double alpha;
   ....
};
...
int main() {
   IntDE myIntegrator;
   Parameter myParameter;
   myParameter.count=....
   ....
   myIntegrator.parm=&myParameter;

普通の変数では，こんなことはできません．もし, myIntegrator.parm=count  が可能なら，myIntegrator.parm は整数型でなければなりませんし, myIntegrator.parm=myParameter  が可能なら，myIntegrator.parm はParameterクラスである必要があります．両者は，並立できないです．ポインターを使うことにより, 「myIntegrator.parmは，方角（住所）」である，と定義できます．東京スカイツリーと，プレハブのボロ屋は，決して互換性がないです(入れる人間の数も違うし，質量も高さも異なる)が，東京スカイツリーの住所と，プレハブのボロ屋の住所は，同じもの「住所」です．それを記録するには，せいぜい30文字の入力欄があれば良いのです(東京スカイツリーの住所欄には耐荷重5000万トンが必要，ということにはならない)．こうやって，多種多様なデータを統一的に表現できるわけです．

だがちょっと変ですね．上では，doubleのポインターはdouble*型,   Parameterのポインターは Parameter* 型ですので，同じではない感じです．これは, 「何の住所かは知らないけど，とりあえ〜ず住所」というvoid* 型というのがあるのです．だから, ここの void *paramというのは, 「とりあえ〜ず住所であることは確定」している param という変数．です．

じゃ，「とりあえ〜ず住所」のままでは，ダメなのでしょうか．もしそれが，Parameter *であったとするなら, そいつには, countとかalphaとかが，あるはずなんですよね．で，それを使いたい．でも, もしかすると size_t* かもしれない，という状態では，countやらalphaってのがある，が，わからないです．

キャスト

そこで，ポインターの利用で重要なキャストを学びましょう．キャストとは，ある変数を，別の型の変数として考え直してみる，という演算です．これを使うと，「それが何かは知らないが，とりあえず住所」を，「Parameterクラスの，とあるインスタンスの住所」に変更できます：

auto v=myIntegrator.Integrate([](double x, void *param) {
      auto& P=*static_cast<Parameter*>(param);   // 昔は，手っ取り早く  P=*(Parameter*)param と書いてもOKであった
      P.count++;
      return 1.0 / std::sqrt(x * (1.0 - x)); 
  }, 0.0, 1.0, err);

ここのstatic_cast<Parameter*>(param)で, 「正体不明の住所」が, 「Parameterクラスの，あるインスタンスの住所」になります．で．先頭に＊がついているので，「Parameterクラスの，あるインスタンスの住所に住んでいる人」つまりインスタンス本体になります．だが，この＆ってのが，何だかわからないですよね・・・こういうのは for(auto& v:SET) のように，意味不明なまま，時々ついていました．そろそろ，その正体を勉強しましょう．

参照

理解するために，このコードが何をしているのか解説しましょう：

class Parameter {
public:
    size_t count;
    Parameter(){count=0;}
} myParm;
...
myIntegrator.parm=&myParm;
auto v=myIntegrator.Integrate([](double x, void *param) {
      auto& P=*static_cast<Parameter*>(param);   // 昔は，手っ取り早く  P=*(Parameter*)param と書いてもOKであった
      P.count++;
      return 1.0 / std::sqrt(x * (1.0 - x)); 
  }, 0.0, 1.0, err);

やりたい内容は，これで，「数値積分するために，何回関数を呼び出したか」を積算したいのです．1回関数を呼ぶたびに, Parameterインスタンスのcount が1増えるわけね．で，Parameterクラスの最後に，ついでにインスタンス myParm を作成してます．まあ，こういう書き方もできる．ということです．なお, インスタンス起動時に, countを0に設定していますね！ここは前回説明した通りで，ここで設定したポインターが, ここに出現するように森先生のプログラムは書かれている．この方法であれば，森先生がご逝去してるんだけれども（つまりIntDEを改造できないんだけど），その後も，どんな構造のパラメータでも，被積分関数に与えることができる. 

で，問題のこのあたりだが，&の意味がわからないので，こうやってみよう:

auto P=*static_cast<Parameter*>(param);

これなら意味はわかる．「何だか知らんが, 何かの住所のparm」を，「Parameterクラスの，あるインスタンス（ここで与えているので myParm のこと）の住所」に変換し，＊をつけて, 「Parameterクラスの，あるインスタンスの住所に住んでいるインスタンス」つまり, myParm になる．だから，ここは，

auto P=myParm;
P.count++;

と書いているのと同じである．で，呼び出し回数を1増やしたのね．

で，これではダメなのです．ここで説明した通り，＝ってのは，「右辺の値の複製を作成し，左辺の値とする」ものです．たとえば，君が友達に授業のノートを借りて，そのコピーを作成し，コピーをお家に持って帰った．という感じです．だとすると，ここは，「友達のノートのコピーに，君が落書きをした」ことに対応します．では，君が自分のコピーに落書きした瞬間に，オリジナルの友達のノートつまりこれに, 君の書いた落書きが出現するでしょうか？出現したらオカルトですよね・・・特殊な能力の持ち主ですよね．なので，Pに操作しても無駄なのです．

じゃあ，友達のノートに，「この関数，1回呼び出されたよ〜」と正の字を書き足すには，どうしたら良いのでしょう？それが，「コピーではない，本物」を意味する参照なのです．こう書きます:

auto& P=*static_cast<Parameter*>(param);

本物，つまり, myParmのコピーではなく，本物を「Pと呼んで参照しまーす」と宣言しているのです．

for(auto& v:SET) v=0 を, for(auto v:SET) v=0 と書くとダメなこともわかります．後者では，① SETの各要素のコピーvを作成せよ．②その値を0とせよ. ③コピーを破棄せよ．と書いたことになります．こんな作業で, SETの値が操作できるわけないです．コピーか？本物か？は，初心者には大変わかりにくいので，がんばりましょう

ラムダ式の定義の[&]

もともとのプログラムでは，Parameterクラスの参照を使ってないですよね：

   ...
   size_t count=0;
   double err,err_req=1e-6;
   myIntegrator.Initialize(err_req); // 初期化
   auto v=myIntegrator.Integrate([&count](double x, void *param) {
       count++;
       return 1.0 / std::sqrt(x * (1.0 - x)); 
   }, 0.0, 1.0, err);

その代わり，ラムダ式の定義に，奇妙な[&count]があります．これは,

  • [&count] ラムダ式を定義する際に，そこから見える count の参照を，関数に持込め

という指示です．なので，この関数のここらで使っているcountは, ラムダ式を定義するときに見えていたcount, すなわち，こやつの「コピーではなく，本物」です．なので，手っ取り早く，関数の呼び出し回数が計算できたわけです．これ以外にも, ラムダ式の[]は使えますよ：

  • [*count] ラムダ式を定義する際に，そこから見える count のポインターを，関数に持込め
  • [count] ラムダ式を定義する際に，そこから見える count のコピーを，関数に持込め

ポインターのメンバー

参照を使わなくても, 本物の値を変更することは可能です．ようするに, *POINTERが本物なので, (*POINTER).count と書けば，問題ないです．で，参照が登場する前は，これしか書けなかったので，略記で POINTER->count と書いて良いことになっています．少し昔のC/C++プログラムを見ると, -> ばかりで面食らうでしょう（大変読みにくいんで・・・）

ポインターはC言語で1970年ごろ発明され，強力便利で広がったのですが，とにかくハッキングに弱いという欠点があり，現在では駆逐対象の文法です. C++は古い言語なので，結構利用する局面があるでしょう．

ポインターを利用した多数のPCウイルスに怒り狂ったMicrosoftは, C言語からポインターを取り除き，存在しないものは使えないというC#言語を発案し，それでWindowsを記述できるように.NETを開発しました．Windowsが兎にも角にも動作しているところを見ると，ポインターって，本当に必要ないんですね．でもDelegateがむやみに難しいんだけど

参照は，ポインターの代わりとして，新しいプログラミング言語では広く使われています．

参照が引数の関数

参照を利用すると，関数の引数に与えた変数を変更できます．普通の関数では

int my_func(double x,double y){....}

となっており, xとyは「引数」であって，その値がmy_func()の実行で変化しません．my_func()の実行中に

x=x+1;

と行っても，my_func()が保有する「xのコピー」の値が変化するだけで，呼び出し元のオリジナルxとyの値は変化しません．ところが！

int your_func(double& x, double &y){....}

のように, xとyの参照を引き渡すと話が違います． your_func()の実行中に

x=x+1;

のように，xの値を変化させると・・・なんせ参照なので，呼び出し元のオリジナルxとyの値も変化してしまいます．なにせオリジナルを渡してしまったので，z=your_func(x,y)を実行すると, zが得られるだけではなく，x, yの値が変化するという挙動をしてしまいます．便利ではありますが，

z=your_func(1.0, 2.3);

みたいに，変数ではないもののオリジナルを渡そうとすると「いやそれ変数じゃねえし」とエラーしますので，注意しておいてください．上のIntegrateの引数のerrは，この仕組みを使って，推定精度を呼び出し元に返却しています．

まあしかし，なんですな．関数の値を知りたいと思って\(z=F(x,y)\)を行ったら，\(z\)だけではなく\(x\)や\(y\)の値が変化してたら，普通の人は怒るだろうな

GITブランチ間のマージ

さて, 練習のために複数のブランチで作業したので，こんな感じになってしまってると思います：

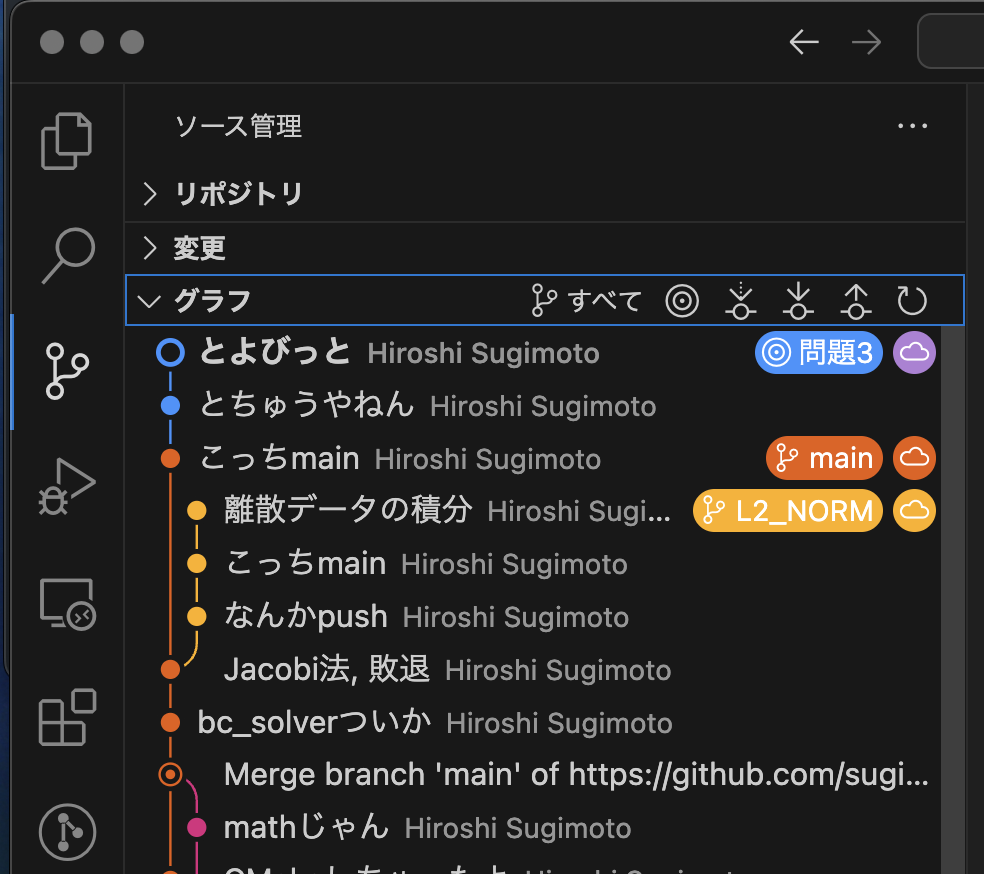
上の例では, 【問題3】ブランチと，【L2_NORM】ブランチで別個の開発が進行しています．【main】ブランチは，結構過去の状態を保持している．

【問題3】ブランチと，【L2_NORM】ブランチの開発を統合しましょう．

まず，統合先のブランチに移動します. 今回は【L2_NORM】ブランチに統合しましょう．で，

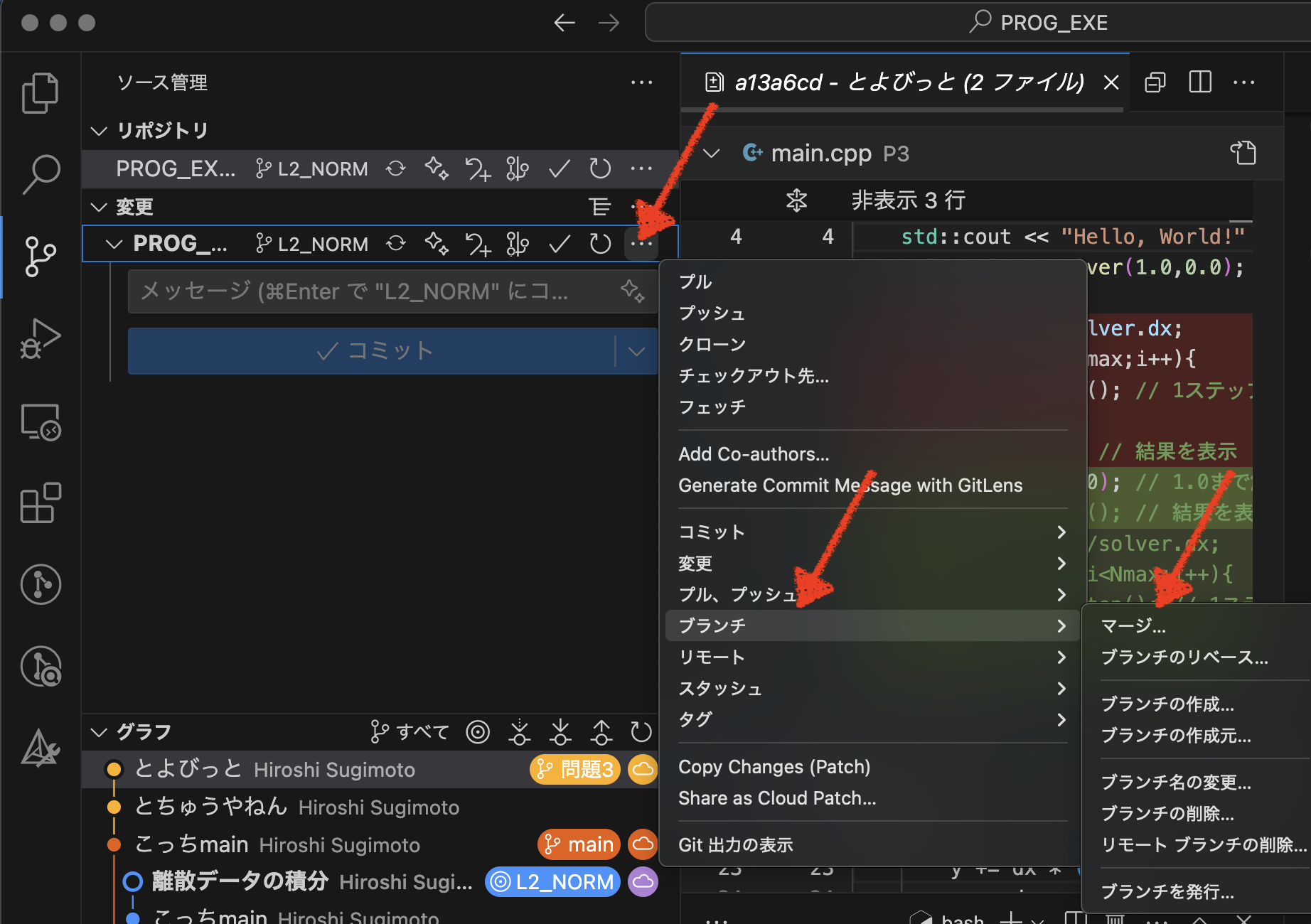
【マージ】を選択. すると, マージする相手のブランチを選ぶ画面が出て，

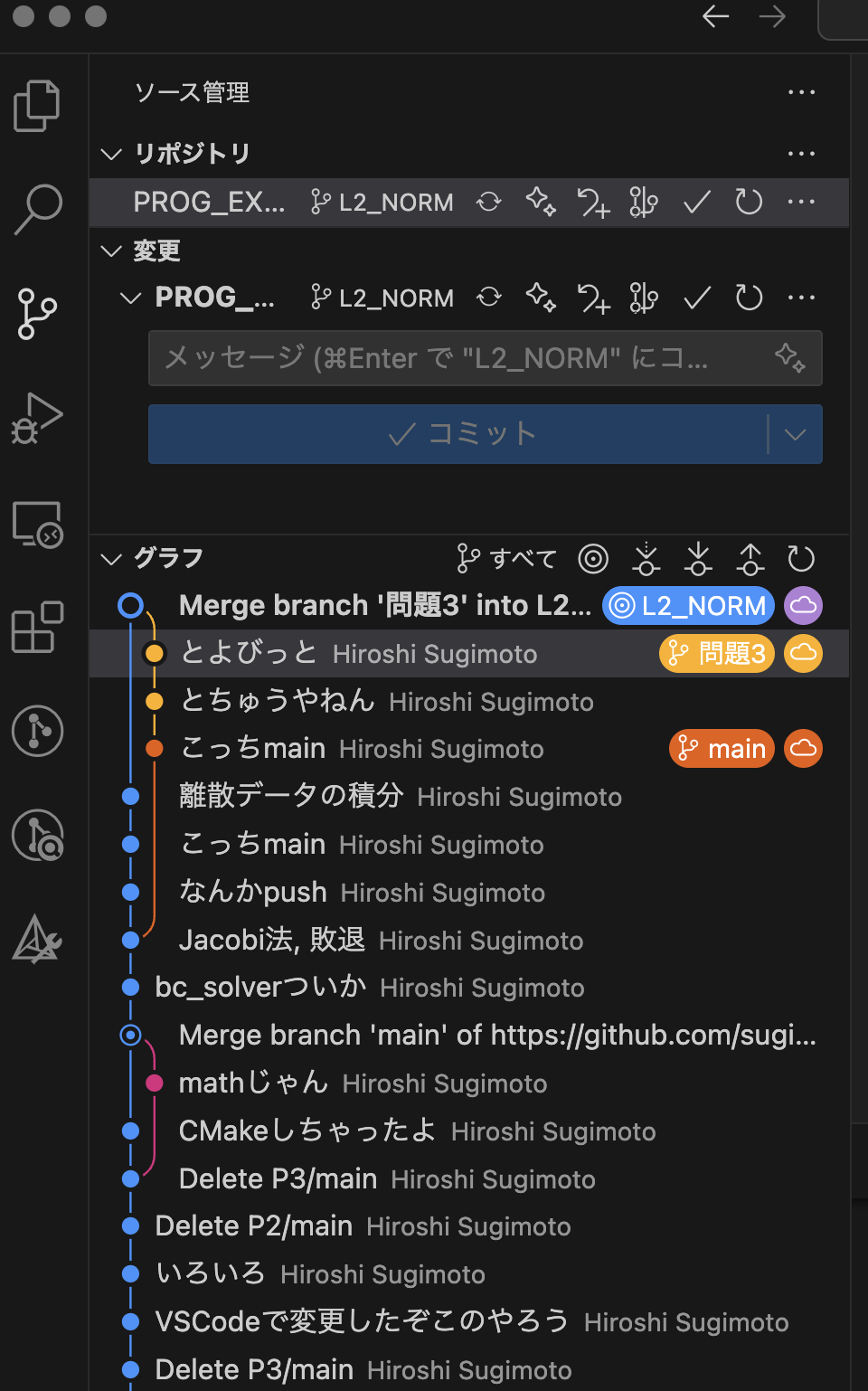
こうなる. 

問題は，2つのブランチで同一箇所を変更しているときである．

コンフリクトの解決

二つのブランチで，同じ部分を違うように変更しているのをコンフリクトといいます．コンフリクトが見つかると，

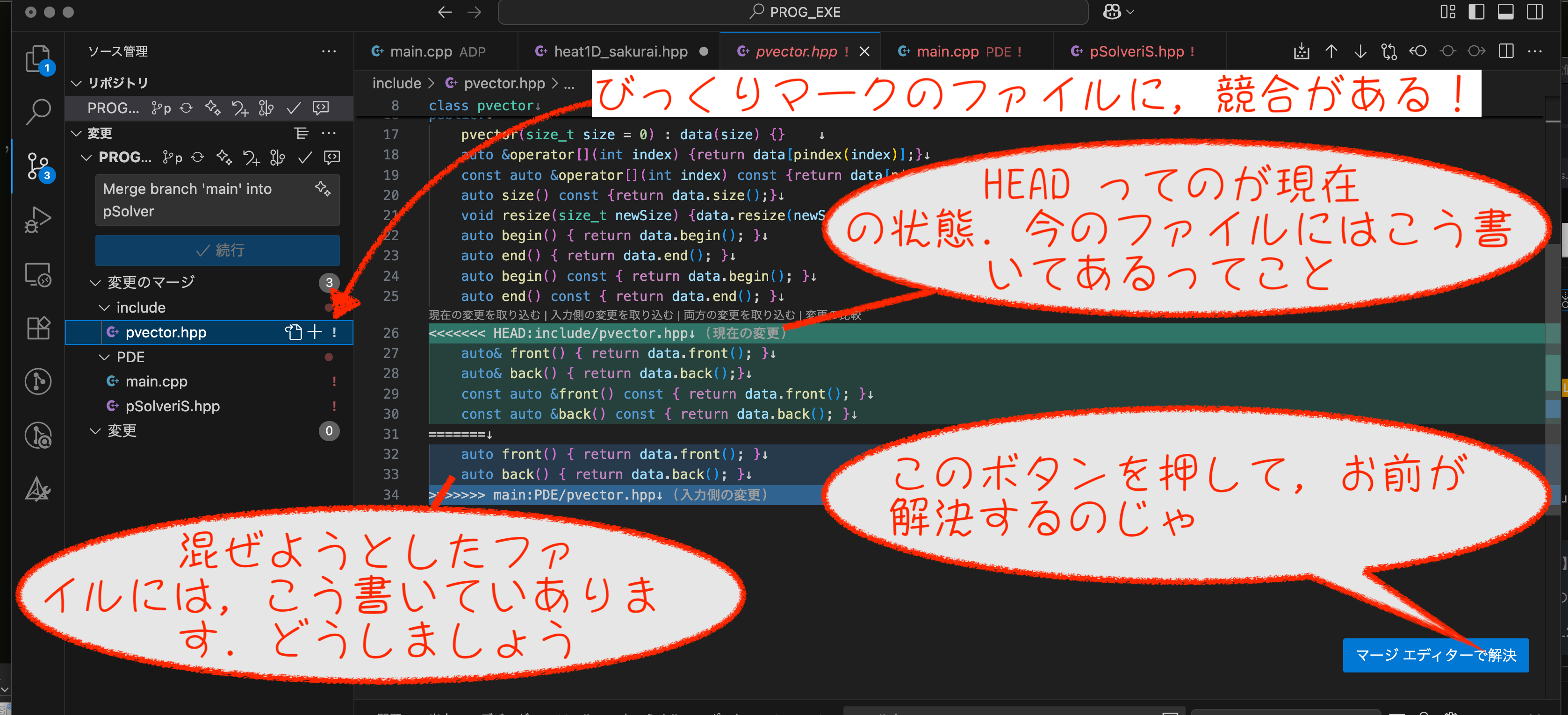
こうなるので，「マージエディタ」で解決しましょう．

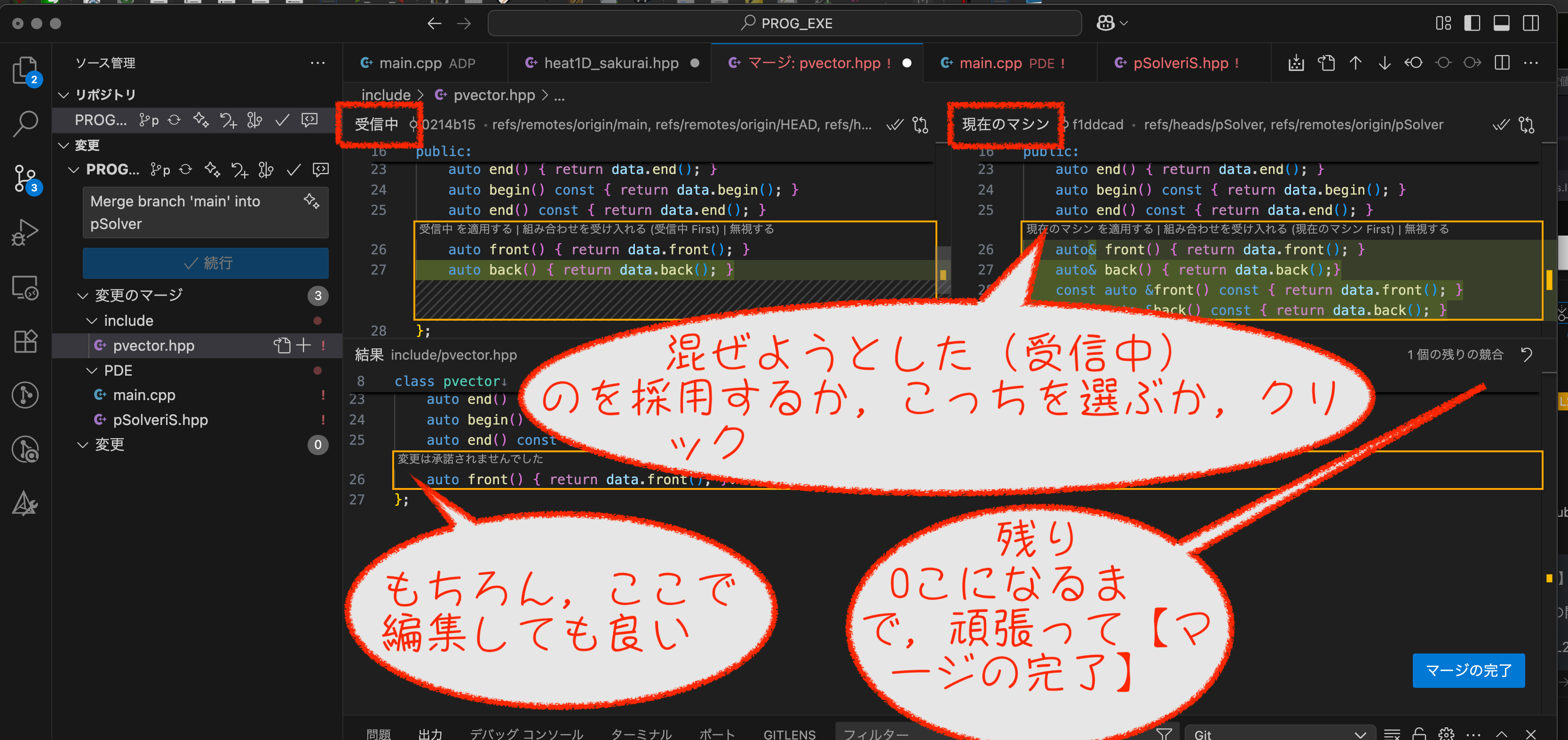
添付 サイズ
intde_0.zip 5.48 KB