法仏型方程式いやこりゃありがてえや
熱伝導方程式
熱伝導方程式(拡散方程式)\[\frac{\partial u}{\partial t}=\kappa\Delta u\tag{1}\]を, 初期値・境界条件つきで時間発展を追うことを考えましょう.
1Dケース
\[\frac{\partial u}{\partial t}=\kappa\dfrac{\partial^2\,u}{\partial x^2}\]ですね. ここでは\(0<x<1\)として, 初期値と境界条件を\[\lim_{t\to 0} u(t,x)=g(x),\qquad \lim_{x\to 0}u(t,x)=U_0,\qquad \lim_{x\to 1}u(t,x)=U_1\]としましょう. 普通に差分してみましょう. \(u_{n,i}=u(\Delta_t n,\Delta_x i)\)として
陽解法
\[\dfrac{u_{n+1,i}-u_{n,i}}{\Delta_{t}}=\kappa\dfrac{u_{n,i+1}-2u_{n,i}+u_{n,i-1}}{\Delta_{x}^{2}},\ \left(0<x_{i}<1\right)\]すなわち\[u_{n+1,i}=Du_{n,i+1}+\left(1-2D\right)u_{n,i}+Du_{n,i-1}\]\[D=\dfrac{\kappa\Delta_{t}}{\Delta_{x}^{2}}\tag{2}\]
この\(D\)を, 拡散に関する拡散数と呼びます. 差分式をよくみると,\[D>\dfrac{1}{2}\tag{3}\]の場合,係数が負のものが現れるので, 陽解法で係数が負は雰囲気やばそうです. 実際, Fourier解析すると, 安定解が保証できないことを確かめることができるでしょう.いや,ここはプログラム教室だから,プログラムを組んで確かめるべきなのか・・・
陰解法
陽解法では1次元しか解けないので, 2次元問題を行う前に, 陰解法も練習しましょう. \[-Du_{n+1,i-1}+(1+2D)u_{n+1,i}-Du_{n+1,i+1}=u_{n,i}\]ですね.境界条件と一緒に行列で書くと,\[\def\vp{\phantom{\sum_{1}^{2}}}
\begin{bmatrix}1 & 0 & & & & \vp\\-D & 1+2D & -D & & & \vp\\& -D & 1+2D & -D & & \vp\\& & \ddots & \ddots & \ddots & \vp\\& & & -D & 1+2D & -D\\& & & & 0 & 1\end{bmatrix}\begin{bmatrix}u_{n+1,0}\vp\\u_{n+1,1}\vp\\u_{n+1,2}\vp\\\vdots\vp\\u_{n+1,N-1}\\u_{n+1,N}\end{bmatrix}=\begin{bmatrix}U_{0}\vp\\
u_{n,1}\vp\\u_{n,2}\vp\\\vdots\vp\\u_{n,N-1}\\U_{1}\end{bmatrix}\tag{4}\]こういう三重対角行列はここで練習しましたね!
ここでは,より一般な,「Sparse Matrix」として解いてみましょう.
SPARSE Matrix
疎行列というのは, まばらにしか非ゼロ要素が存在しない行列です.

まあでも, 数値シミュレーションに出現する疎行列では,対角要素はゼロではない,という条件がつくのが多いです.疎行列の困ったちゃんなところは, 「疎行列を解こうとして未知数を消去(つまりLU分解)していったら,密行列になっちゃうかもよ」という点です.
\[\begin{bmatrix}\ 1\ & -1 & -1 & -1 & -1 & -1\\ 1 & 1\\ 1 & & \text{1}\\ 1 & & & 1\\ 1 & & & & 1\\ 1 & & & & & 1 \end{bmatrix}\to\begin{bmatrix}\ 1\ & -1 & -1 & -1 & -1 & -1\\ 0 & 2 & 1 & 1 & 1 & 1\\ 0 & 1 & 2 & 1 & 1 & 1\\ 0 & 1 & 1 & 2 & 1 & 1\\ 0 & 1 & 1 & 1 & 2 & 1\\ 0 & 1 & 1 & 1 & 1 & 2 \end{bmatrix}\]
疎行列が溢れた・・・このままじゃ俺の計算は全滅じゃあ〜〜
落ち着いてミト!あれは・・・Eigenに向かって飛べ!
最初の疎行列ならメモリーに格納できたが,解こうとして右辺の行列になったら密行列で,計算機がダウン!というわけです.疎行列自身の要素数(=計算機パワー)は十分小さくても,連立方程式を解こうとしてLU分解を始めると,要素数が爆発して計算機パワーを凌駕してしまうわけね.
しかし,まあ数値シミュレーションに出現する疎行列では,ブロック状に0行列が出現することが多い:
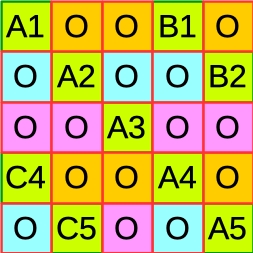
この場合,理屈で言って「ここゼロだし」ということが分かることも多いわけで,そこを回避するようにプログラムを組むわけです.上の例だと, A1-B1ブロックとC4-A4ブロックの計算では,オレンジ部分はずっと0のままである.だが,それは,問題によってプログラムが特注品になる,ということでもあります.だから,頑張ってね.ただし,
- Eigenには, 疎行列を取り扱うためのライブラリーがあるみたい
なので,使ってみましょう!
基底クラス
まずは基底クラスですよね!有界領域で空間1Dなので, こんな感じかな. ほとんどpSolver1DBase.hpp と同じだが
// bSolver1DBase.hpp Solve some equation using some method. Bounded region #pragma once #include <iostream> #include <filesystem> #include <cmath> #include <vector> #include <fstream> #include "../include/pvector.hpp" template <typename T> class bSolver1DBase { protected: double C = 1.0, K=1.0; // Cは速度、Kは拡散係数 double CFL, DN; // CFL条件と拡散数 double dt, dx, time, xmax = 1.0; int nt = 0; // 時間ステップのカウンタ double LBC_value = 0.0; // 下端の境界条件の値 double RBC_value = 0.0; // 上端の境界条件の値 class Point { public: Point *pre = nullptr; // ポインタを追加して前のポイントへのリンクを作成 Point *next = nullptr; double X; pvector<T> U; // U_n Point() : U(3) {} // デフォルトコンストラクタでサイズ3のpvectorを初期化 auto &operator[](int index) { return U[index]; } const auto &operator[](int index) const { return U[index]; } }; std::vector<Point> Data; std::ofstream ofs; public: bSolver1DBase(const size_t &nx, const double &dt, const std::function<double(double)> &U0) : dt(dt) { time = 0.0; // 初期時間 dx = xmax / nx; // 空間刻み幅の計算 CFL = C * dt / dx; // CFL条件の計算 DN = C * dt /dx/dx; // 拡散数の計算 Data.resize(nx+1); // 空間分割数に基づいて初期化 for (size_t i = 0; auto &P : Data) { P.pre = &Data[i - 1]; P.next = &Data[i + 1]; P[nt] = P[nt - 1] = P[nt - 2] = U0(P.X = i * dx); // 初期条件の適用 i++; } std::cout << "Booting bSolver1DBase with nx=" << Data.size() << ", dt=" << dt << std::endl; } std::string what() const { return "nSolver1DBase: nx=" + std::to_string(Data.size()) + ", dt=" + std::to_string(dt) + ", CFL=" + std::to_string(CFL) + " , DN=" + std::to_string(DN) + ", time=" + std::to_string(time); } double& LBC() { return LBC_value; } // 下端の境界条件 double& RBC() { return RBC_value; } // 上端の境界条件 bool Write(const std::string &filename) { if (ofs) ofs.close(); // 既存のファイルストリームを閉じる std::filesystem::path datafile = getenv("HOME"); datafile /= filename; std::filesystem::create_directories(datafile.parent_path()); ofs.open(datafile); if (!ofs) throw std::ios_base::failure("Failed to open file: " + datafile.string()); return Write(); } bool Write() { try { ofs << std::endl << "# nt= " << nt << " time= " << time << " CFL= " << CFL << " NX= " << Data.size() << std::endl; for (auto &v : Data) ofs << v.X << " " << v[nt] << std::endl; } catch (const std::exception &e) { std::cerr << "Error writing to file: " << e.what() << std::endl; return false; } std::cout << "time[" << time << "]written to file successfully." << std::endl; return true; } virtual void Step(double U_W = 0.0) = 0; virtual void Initialize(void *parm = nullptr) {}; double get_time() const { return time; } };
まあ名前が違うところ以外は, ここいらで拡散係数などを定義.ここはフツーのstd::vectorで, でも格子点が0,1,...,NX+1 であると, 区間幅は0,1,...,NX になるから, ここの数が1個違うだけ. 人によっては,pSolver1DBase と bSolver1DBase の共通のご先祖様 Solver1DBase から派生した方がいいと思うかもだな.
あ,ここは!先ほど別のプログラムで作成した pvector.hpp ですね.こういう,よく使う汎用プログラムは,共通のフォルダーを作って,そこに入れておくのが良いです.
include/ というフォルダーが多いかな? lib/ もありだが.
で, この辺は,有界領域の問題なので, 上下で境界条件を設定したくなるかもなあ.というものです.このあたりは, まあ今は使いませんが,のちのち, コンストラクタとStep()の間に作業が入るようになるかもしれないので,念の為に作ってあります.
Explicit
基底クラスがよくできてれば,派生クラスは簡単です
// heat1D_explicit.hpp
#pragma once
#include "bSolver1DBase.hpp"
class Heat1DExplicit : public bSolver1DBase<double>
{
public:
Heat1DExplicit(const size_t &nx, const double &dt, const std::function<double(double)> &U0 = [](double x)
{ return 0.; }) : bSolver1DBase<double>(nx, dt, U0)
{
std::cout << "Starting Heat1DExplicit solver with nx=" << Data.size() << ", dt=" << dt << std::endl;
}
void Step() override
{
Data[0][nt + 1] = LBC_value; // 下端の境界条件
Data[Data.size() - 1][nt + 1] = RBC_value; // 上端の境界条件
for (size_t i = 1; i < Data.size() - 1; ++i)
Data[i][nt + 1] = (1.-2.*DN)* Data[i][nt] + DN * (Data[i - 1][nt] + Data[i + 1][nt]);
time += dt;
nt++;
}
};
// heat1D_explicit.hpp(2)式を書いただけ,ですね.これでmain()は
// main.cpp
#include "heat1D_explicit.hpp"
int main()
{
size_t nx = 20; // 空間分割数 100(text), 40, 20, 8
double dt = 0.1 / nx /nx; // 時間刻み幅
size_t ntmax = 5. / dt; // 最大時間ステップ数
size_t ntsave = .005 / dt; // データ保存間隔
std::string filename = "Data/test04/CDE_20.dat";
Heat1DExplicit mySolver(nx, dt);
mySolver.LBC() = 1.0; // 下端の境界条件
mySolver.Initialize();
mySolver.Write(filename);
for (size_t nt = 0; nt < ntmax; nt++)
{
mySolver.Step(); // 時間ステップを実行
if ((nt + 1) % ntsave == 0)
mySolver.Write();
}
return 0;
}ここは(3)にならないように書きました!境界条件を左が1に設定!細かめにデータ保存したら, 左みたいになっちまったorz (一応収束していることは,わかる.でも,こんな図を課長に見せたら「最後どうなってんのか見えねえぞ,帰れ」となってしまう)ので,ここいらへんを改造して右図みたいにしましたとさ.
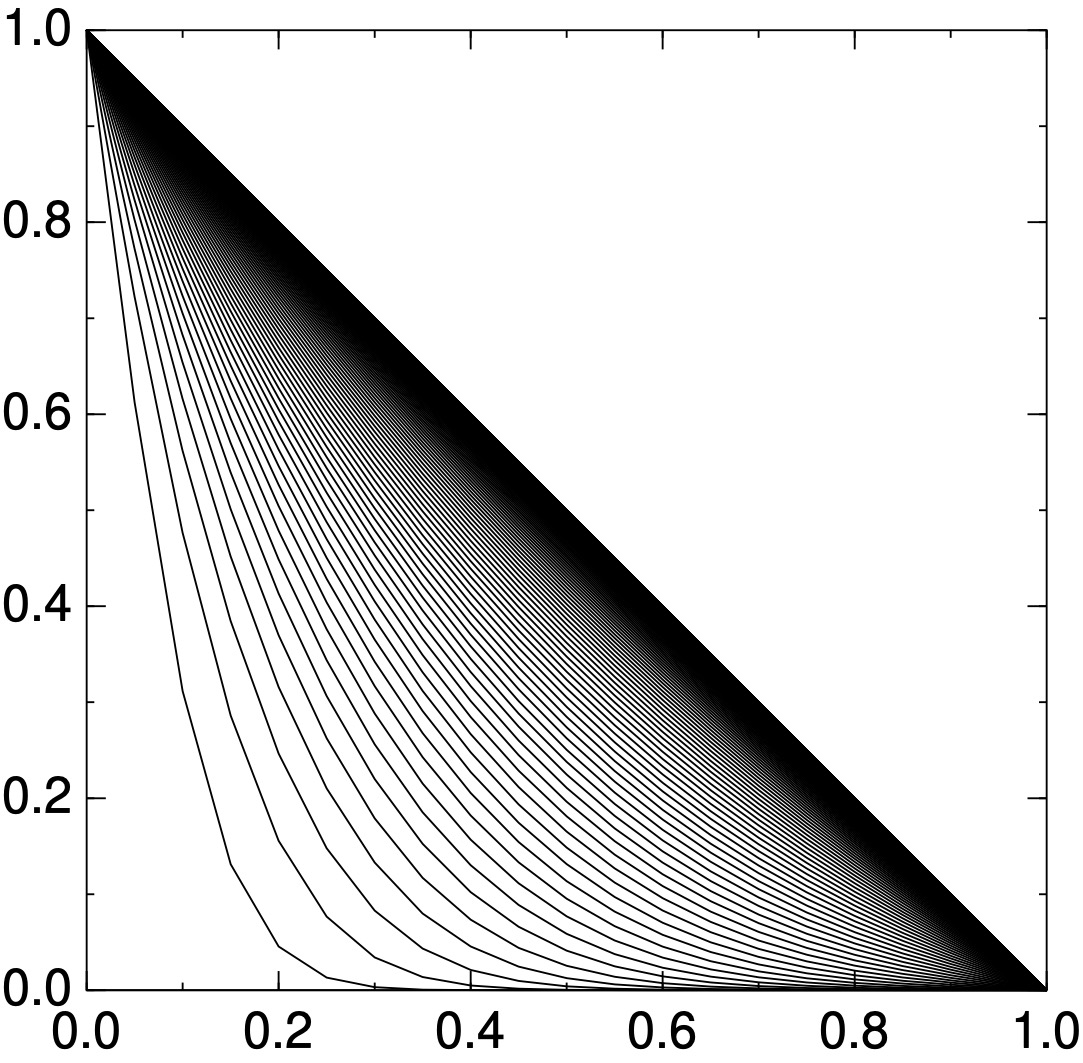
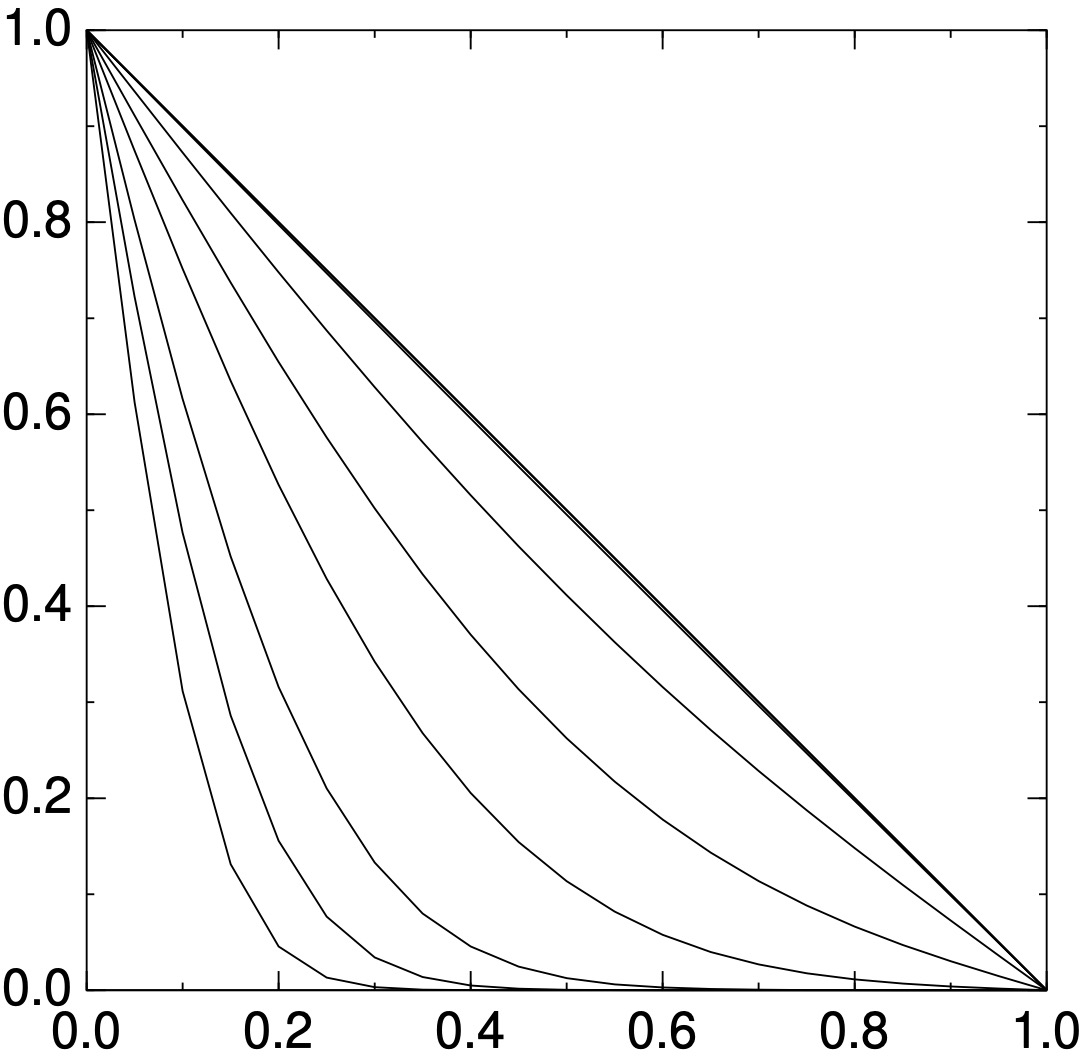
改造はこんな感じにしてみた:
#include <set>
...
std::set<int> tset;
tset.insert(round(0.005/dt));tset.insert(round(0.010/dt));tset.insert(round(0.020/dt));
tset.insert(round(0.050/dt));tset.insert(round(0.10/dt));tset.insert(round(0.20/dt));
tset.insert(round(0.50/dt));tset.insert(round(1/dt));tset.insert(round(2/dt));
tset.insert(round(5/dt));
...
for (size_t nt = 0; nt < ntmax; nt++)
...
if (tset.contains(nt+1))
mySolver.Write();なんで整数にしてるんだ? という点ですが, 最初double でやったら,2とかが1.999999999999999 になって, 「2.00000000000000001じゃないから保存しないもん」になったからです.このように, double 数値を A=B とか A>B とかで比較すると,たまにハマる.というのは鉄則なので, 覚えておくと良いです.
陽解法は1Dだと解けますね!でもnt=20000までかかっています.
Eigen/SPARSEの 使い方
Eigen/SPARSEの使い方をimplicitスキームの構築で学びましょう. (注意: EigenのVersion 3.4.0を利用してくださいね. EigenのVersionの確認方法は, 猿に聞け)
// heat1D_implicit.hpp #pragma once #include "bSolver1DBase.hpp" #include <Eigen/Sparse> class Heat1DImplicit : public bSolver1DBase<double> { Eigen::SparseLU<Eigen::SparseMatrix<double>> solver; public: Heat1DImplicit(const size_t &nx, const double &dt, const std::function<double(double)> &U0 = [](double x) { return 0.; }) : bSolver1DBase<double>(nx, dt, U0) { std::cout << "Starting Heat1DImplicit solver with nx=" << Data.size() << ", dt=" << dt << std::endl; } void Initialize(void *parm = nullptr) override {
Eigen::SparseMatrix<double> coef; // スパース行列を使用して係数行列を表現
coef.resize(Data.size(), Data.size());
for (int i = 0; i < Data.size(); i++) { if ((i==0)||(i==Data.size()-1)) // 境界条件の処理 coef.insert(i,i) = 1; else { coef.insert(i, i - 1) = -(DN + 0.5 * CFL); // 左隣の成分
coef.insert(i, i) = 1. + 2. * DN; // 対角成分だにゃ
coef.insert(i, i + 1) = -(DN - 0.5 * CFL); // 右隣の成分
}
} coef.makeCompressed(); // スパース行列を圧縮
solver.compute(coef);
if (solver.info()!=Eigen::Success)
throw std::runtime_error("Error::Heat1DImplicit::Initialize::Can not solve fuck.");
std::cout << "Heat1DImplicit solver initialized with nx=" << Data.size() << ", dt=" << dt << std::endl; } // 時間ステップを実行するメソッド void Step() override {
Eigen::VectorXd b(Data.size());
for (int i = 0; i < Data.size(); i++)
if (i == 0) b[i] = LBC_value; // 下端の境界条件
else if (i == Data.size() - 1) b[i] = RBC_value; // 上端の境界条件
else b[i] = Data[i][nt]; // 現在の値を設定
auto result=solver.solve(b); // 連立方程式を解く time = (++nt) * dt;
for (int i = 0; i < Data.size(); i++) Data[i][nt] = result[i]; } }; // heat1D_implicit.hpp
これでEigen/Sparseを読み込みます. まずはLU分解を入れておくところを用意. で, Initialize()で,(4)の行列を作成します.まずはこうやってSparse行列と, そのサイズを設定します.
ここでは1行目とN行目の対角成分を1に設定. この見慣れない||は, 二つの条件の論理OR(どちらかがtrueならtrue)を意味しています. なお, AND(どっちもtrueならtrue)は && です.
なんで | と & ではないのか?試しに書いてみると動くんだが?という向きのために説明しておくと, | は bit-OR つまり二進数で 0101 と 1001 なら 1101 になる,という計算になってしまいます.&も bit-ANDで, 0101 & 1001 = 0001 になります.で,たまに論理OR, 論理ANDと結果が一致していると,動いている気がする,というわけです.この説明がわからん,という人は,黙って || と && と書いてくださいね!
この辺では, i行目の成分として, i-1列目, i列目, i+1列目を設定します.Eigen/Sparseは, こうやって「値を設定」したあと, このmakeCompressedで計算機メモリーを節約します.さて,設定した行列をLU分解しておけば計算が速くなります.ここで必ずやっておきましょう!で, LU分解はいつでも可能ではなく,失敗する場合がありますので,こうやって失敗を検出しておきましょう.
さて, 時間ステップ Step() では, 計算を行います.
では連立方程式\(\mathsf{A}\boldsymbol{x}=\boldsymbol{b}\) \(\mathbf{b}\)ベクトルを設定します.で,これで解けるので, 回収しておきましょう.
ここらへんで解いている最中には,計算機の使用メモリーが上昇します.どれくらい上昇するかは行列に依存しますが,まあ数倍くらいで済むことが多い感じです.
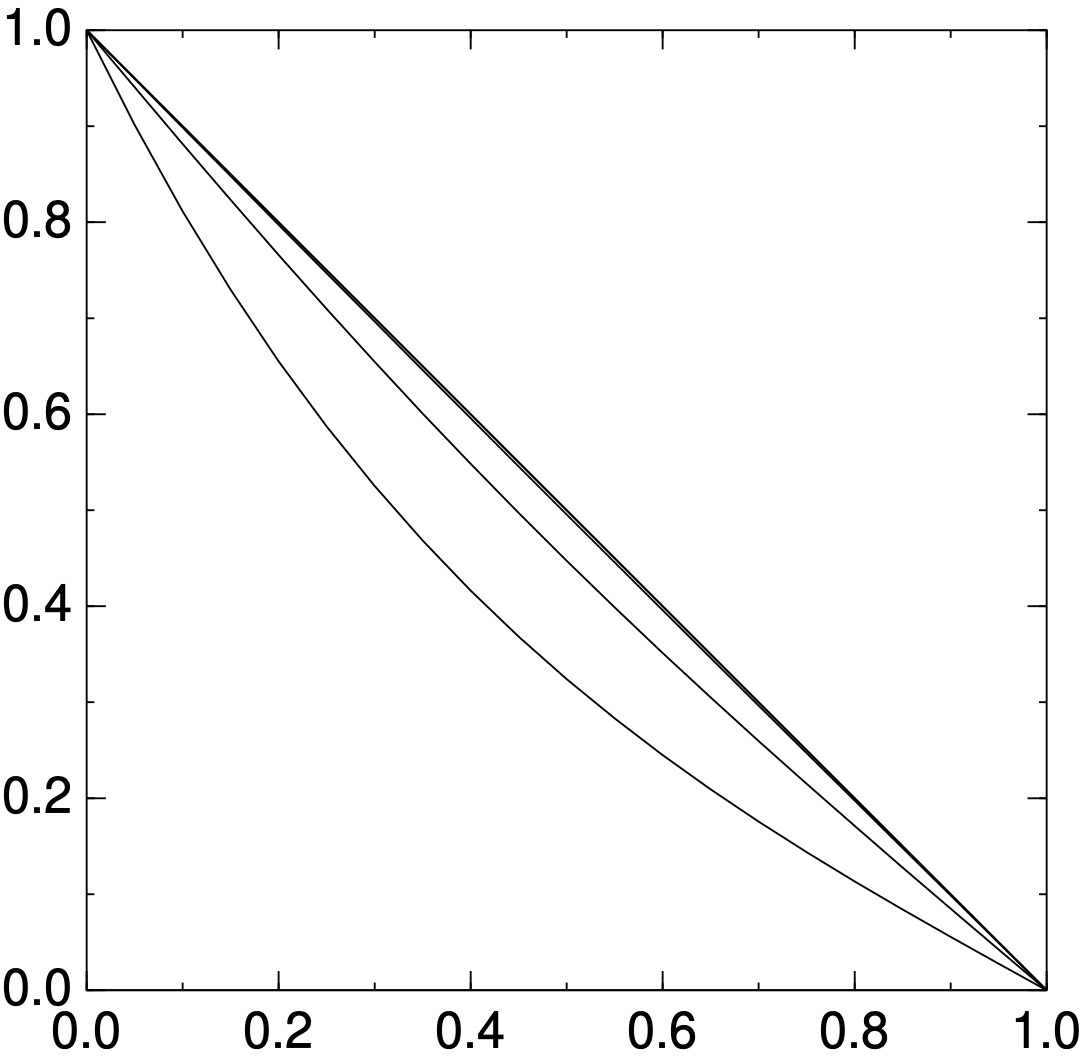 陰解法なので, 時間ステップをいくらでも大きくとれる. この例ではnt=20でt=5まで到達.
陰解法なので, 時間ステップをいくらでも大きくとれる. この例ではnt=20でt=5まで到達.
移流拡散方程式
移流項を追加した拡散方程式を, 移流拡散方程式と呼びます.
境界値問題
1Dだと\[\dfrac{\partial u}{\partial t}+c\dfrac{\partial u}{\partial x}=\kappa\dfrac{\partial^2\,u}{\partial x^2}\quad(0<x<1)\qquad u(t,0)=1\qquad u(t,1)=0\tag{5}\]
まあ通例は定常状態に大きな興味がある. というわけで時間微分は1次精度にしといてImplicitで差分化すると, \[-\left(D+\dfrac{C}{2}\right)u_{n,i-1}+(1+2D)u_{n,i}-\left(D-\dfrac{C}{2}\right)u_{n,i+1}=u_{n-1,i}\] 今やこれは簡単ですね!なお定常状態の解は\[\dfrac{c}{\kappa}\dfrac{\partial u}{\partial x}=\dfrac{\partial^2\,u}{\partial x^2}\ \to\ u(\infty,x)=\dfrac{e^{\omega x}-e^\omega}{1-e^\omega},\ \omega=\dfrac{c}{\kappa}\]ですね.
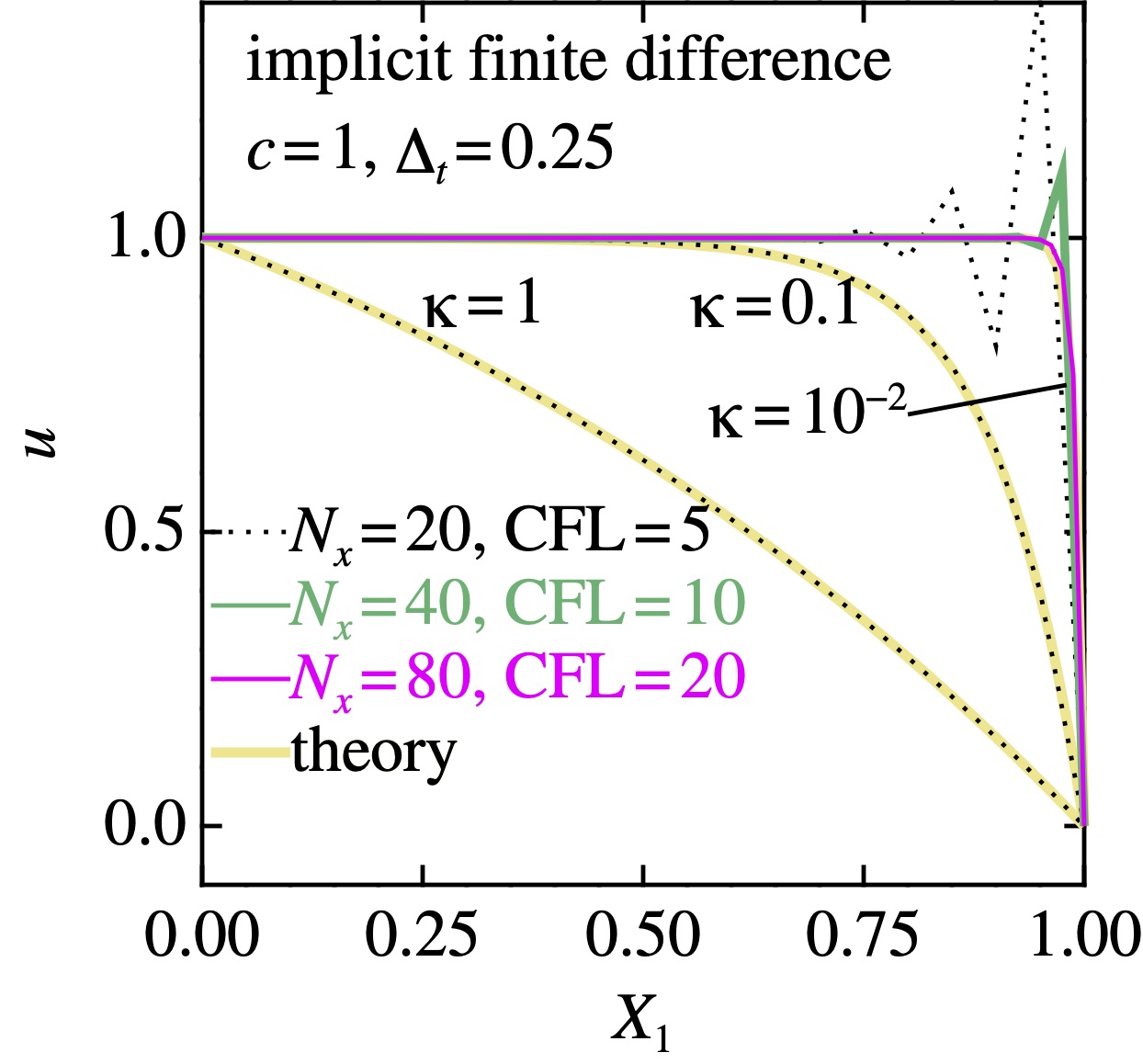
まあ定常解で\(\kappa\)を色々に変えると, こんな感じの結果が出るはず:
おえかき プログラム
こんな感じ:
#!/bin/bash
# fig.sh: 偏微分方程式II: 拡散方程式
. draw.sh
. standards.sh
COLOR=1
X_AXIS='\fIX\sb\fR1\eb'
X_RANGE='0 1 0.25'
Y_AXIS='\fIu'
Y_RANGE='-0.1 1.4 0.5'
OPT="--pen-colors=1=DarkRed:2=MediumSeaGreen:3=Blue:4=Magenta:5=Khaki --symbol-line-width 0.0020"
#(c,κ)の解析解のデータが,ぽっちい〜
echo -e "1 1\n1 1e-1\n1 1e-2\n"|gawk '{
NX=100; dx=1/NX; omega=$1/$2;
for(i=0;i<NX+1;i++)
{
X=i*dx;
Y=(exp(omega*(X-1))-1)/(exp(-omega)-1);# exp(omega)なんて書いたらオーバーフローするき!
printf("%f %f\n",X,Y);
}
printf("\n");
}' > $TMP/steady
#凡例
cat > $TMP/legend.dat <<@
#m=Solid:Black,S=Omit
0.05 1.3 l:implicit finite difference
0.05 1.15 l:\fIc\fR\r8=\r81, \fI\*D\sbt\eb\fR\r8=\r80.25
0.25 0.825 lb:\*k\r8=\r81
0.75 0.95 rt:\*k\r8=\r80.1
0.98 0.75
0.8 0.7 r:\*k\r8=\r810\sp-2\ep
#m=Dot:Black,S=Omit
0.01 0.5
0.10 0.5 l:\fIN\sbx\eb\fR\r8=\r820, CFL\r8=\r85
#m=Solid:Green,S=Omit
0.01 0.375
0.10 0.375 l:\fIN\sbx\eb\fR\r8=\r840, CFL\r8=\r810
#m=Solid:Magenta,S=Omit
0.01 0.25
0.10 0.25 l:\fIN\sbx\eb\fR\r8=\r880, CFL\r8=\r820
@
cat>>$TMP/steady<<@
0.01 0.125
0.10 0.125 l:theory
@
LEGEND=$TMP/legend.dat
LEGEND_OPT="--line-width 0.003"
cat>$TMP/nls<<@
$TMP/steady Solid:Cyan:0.007 Omit
ADi_20_K1.dat.last Dot:Black:0.003 Omit
ADi_20_K1e-1.dat.last Dot:Black:0.003 Omit
ADi_20_K1e-2.dat.last Dot:Black:0.003 Omit
ADi_40_K1e-2.dat.last Solid:Green:0.006 Omit
ADi_80_K1e-2.dat.last Solid:Magenta:0.003 Omit
@
NAMAE=( `cat $TMP/nls|grep -v ^#|gawk '{printf("%s ",$1);}'` )
LINE=( `cat $TMP/nls|grep -v ^#|gawk '{printf("%s ",$2);}'` )
SYMBOL=( `cat $TMP/nls|grep -v ^#|gawk '{printf("%s ",$3);}'` )
draw ADi.pdf ${NAMAE[@]}計算プログラムよりも,こっちがむしろ大変だなwww
周期解
周期解を解いてみましょう. 具体的には, この辺と同じ初期値で解を探してみましょう. 移流部分が入っているので, 時間精度を2次にしてみた:\[\dfrac{u_{n+1,i}-u_{n,i}}{\Delta_{t}}+\dfrac{c}{2}\left(\dfrac{u_{n+1,i+1}-u_{n+1,i-1}}{2\Delta_{x}}+\dfrac{u_{n,i+1}-u_{n,i-1}}{2\Delta_{x}}\right)=\dfrac{\kappa}{2}\left(\dfrac{u_{n+1,i+1}-2u_{n+1,i}+u_{n+1,i-1}}{\Delta_{x}^{2}}+\dfrac{u_{n,i+1}-2u_{n,i}+u_{n,i-1}}{\Delta_{x}^{2}}\right)\]時間微分のところ,同じやないけ?と思う読者のために説明しておくと, これは, \((t,x)=\left(\left(n+\dfrac{1}{2}\right)\Delta_t, i\Delta_x\right)\)という,中途半端なところまわりにTaylor展開して2次精度にしているんですね!で, 解くべき行列は, 例えば拡散方程式の(4)なら,行列の一番上(\(x=0\)の境界条件)を周期条件に書き換えたら良い. 一番下は,では, \(x=0=1\)における方程式に置き換えるのかな?\[\def\vp{\vphantom{\sum_{1}^{2}}}
\begin{bmatrix}
1 & 0 & & &\vp&-1\\
-(D+C/2) & 2(1+D) & -(D-C/2) & & & \vp\\
& -(D+C/2) & 2(1+D) & -(D-C/2) & & \vp\\
& & \ddots & \ddots & \ddots & \vp\\
\vp & & & -(D+C/2) & 2(1+D)& -(D-C/2)\\
\color{magenta}{2(1+D)}&\color{magenta}{-(D-C/2)}& & &\color{magenta}{-(D+C/2)}& \vp
\end{bmatrix}
\begin{bmatrix}
u_{n+1,0}\vp\\
u_{n+1,1}\vp\\
u_{n+1,2}\vp\\
\vdots\vp\\
u_{n+1,N-1}\\
u_{n+1,N}
\end{bmatrix}\]
\[=
\begin{bmatrix}
0\vp\\
(D+C/2)u_{n,0} +2(1-D)u_{n,1} +(D+C/2)u_{n,2}\vp\\
(D+C/2)u_{n,1} +2(1-D)u_{n,2} +(D+C/2)u_{n,3}\vp\\
\vdots\vp\\
(D+C/2)u_{n,N-2}+2(1-D)u_{n,N-1} +(D+C/2)u_{n,0}\vp\\
(D+C/2)u_{n,N-1}+2(1-D)u_{n,0} +(D+C/2)u_{n,1}\vp
\end{bmatrix}
\]これは,まずい. 行列の基本変形で, 1行目を\(-(D-C/2)\)倍したのと, 残りの行の総和を計算すると, 全部0の行になります!\[\def\vp{\vphantom{\sum_{1}^{2}}}
\begin{bmatrix}
1 & 0 & & &\vp &-1\\
-(D+C/2) & 2(1+D) & -(D-C/2) & & & \vp\\
& -(D+C/2) & 2(1+D) & -(D-C/2) & & \vp\\
& & \ddots & \ddots & \ddots & \vp\\
& & & -(D+C/2) & 2(1+D) & -(D-C/2)\\
\color{magenta}{0} &\color{magenta}{0} &\color{magenta}{0}&\color{magenta}{0}&\color{magenta}{0}&\color{magenta}{0} \vp
\end{bmatrix}
\begin{bmatrix}u_{n+1,0}\vp\\u_{n+1,1}\vp\\u_{n+1,2}\vp\\\vdots\vp\\u_{n+1,N-1}\\u_{n+1,N}\end{bmatrix}\]
ってこた,例えば一番下に追加した「\(x=0=1\)における方程式」は, 他の行と独立ではないので,この行列は行列式が0になってます.
- こういう状況で, LU分解とかの系統で数値解析すると,誤差が非常に大きいとか,「行列式0ぢゃん」とライブラリーが文句を言ってきて,解けない
- こういう状況で,Jacobiとかの逐次近似系で数値解析すると,解が確定しないので,ずるずると解が平行移動してずれる現象が起こる.
- だってほれ,正則ではない(=特異な)行列はゼロ空間があるので, とあるベクトル\(\boldsymbol{Y}\)があって, \[(\mathsf{E-A})\boldsymbol{Y}=\boldsymbol{Y}\]になるので,Jacobi法だったら\[\boldsymbol{x}^{(n)}+\varepsilon\boldsymbol{Y}=\left(\mathsf{E-A}\right)\left(\boldsymbol{x}^{(n)}+\varepsilon\boldsymbol{Y}\right)-\boldsymbol{b}\]で\(\varepsilon\)が確定しないんっすよ.
ですが, こういう時には,だいたい「保存」する量があります.(5)を\(0<x<1\)で積分すると, \[\left(\dfrac{\mathrm{d}}{\mathrm{d}t}\int_0^1 u(t,x) \mathrm{d}x\right)
+c\left[u(t,x)\right]_{x=0}^1=\left(\dfrac{\mathrm{d}}{\mathrm{d}t}\int_0^1 u(t,x) \mathrm{d}x\right)=\kappa\left[\dfrac{\partial u}{\partial x}(t,x)\right]_{x=0}^1=0\]つまり\(u\)の総量は時間変化しない \[\dfrac{\mathrm{d}}{\mathrm{d}t}\left(\int_0^1 u(t,x) \mathrm{d}x\right)=0\]です.だから,一番下の行は,\(u\)の総量は時間変化しないということで, 総和が\[S=\sum_{i=0}^{N-1} u_{0,i}\]になるという式に置き換えましょう.さらに,一番上の式で\(u_{n+1,N}=u_{n+1,0}\)がわかってるんだから, 未知数減らそうかな?\[\def\vp{\vphantom{\sum_{1}^{2}}}
\begin{bmatrix}
-(D+C/2) & 2(1+D) & -(D-C/2) & & \vp \\
& -(D+C/2) & 2(1+D) & -(D-C/2) & \vp \\
& & \ddots & \ddots & \ddots \vp\\
-(D-C/2) &\vp & & -(D+C/2) &\vp 2(1+D) \\
\color{magenta}{1}&\color{magenta}{1}&\color{magenta}{1}&\color{magenta}{1}&\vp\color{magenta}{1}
\end{bmatrix}
\begin{bmatrix}u_{n+1,0}\vp\\u_{n+1,1}\vp\\u_{n+1,2}\vp\\\vdots\vp\\u_{n+1,N-1}\end{bmatrix}=
\begin{bmatrix}
(D+C/2)u_{n,0} +2(1-D)u_{n,1} +(D+C/2)u_{n,2}\vp\\
(D+C/2)u_{n,1} +2(1-D)u_{n,2} +(D+C/2)u_{n,3}\vp\\
\vdots\vp\\
(D+C/2)u_{n,N-2}+2(1-D)u_{n,N-1} +(D+C/2)u_{n,0}\vp\\
S\end{bmatrix}
\]
で,やってみると
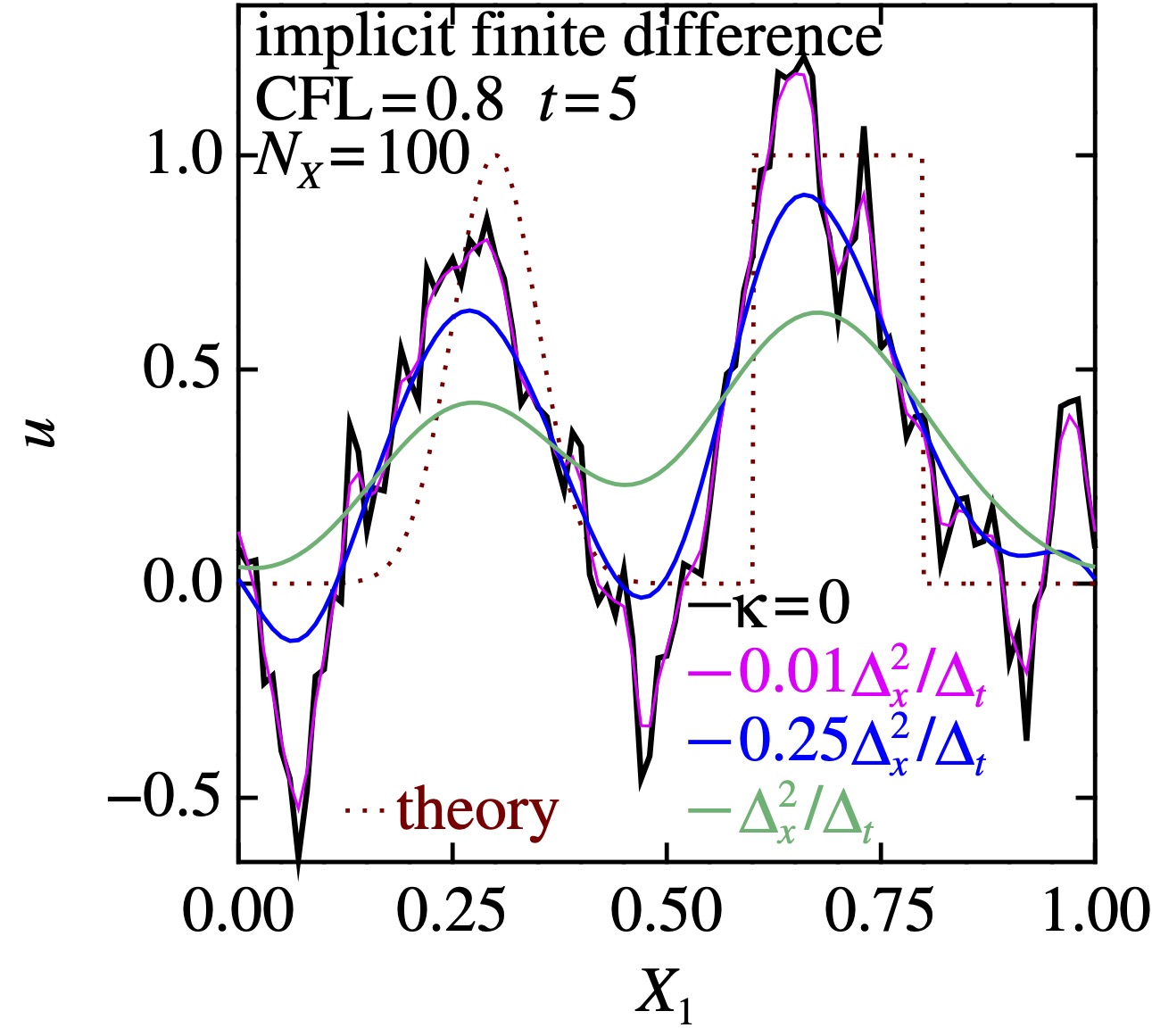
- \(\kappa=0\)の移流方程式だと,なんか解が「ガタガタ」する
- \(\kappa>0\)の移流拡散方程式では, \(\kappa\)が小さいと解の概要はそんなに変わらないが,上の「ガタガタ」が消える
- \(\kappa\)が大きくなると,どんどん,ダラーっとなる
- サンプルのように,\(\Delta_x\to 0\)で\(\kappa\to 0\)になるのなら,オリジナルの伝達方程式を解いていると考えても良い
- こういう, (極限では消えてなくなる)拡散的な項によって「ガタガタ」を抑える方法を, 人工粘性というます.
- まあでも,普通は離散化したとき,勝手に入ってくるナチュラルメークな感じのを人工粘性と呼ぶ.
- この例のように,粘性足りないからって,わざわざ入れて,肌荒れを見えなくするってのは,なんかこう,ファンデーションたっぷりな,あざとい人工粘性と呼ぶべきかも
- ファウンデーションに時間2次精度は贅沢なのでは?と思ったあなた,やってみましょう!ここが1次でよければ逆行列いらねえしな
こうして滑らかな解は得られるのですが,そこで大きな問題が生じます.
- 滑らかだったら,正しいのか.振動する解は,常に誤りなのか.
- 今回は厳密解がわかっているので,厳密解に近くなるように\(\kappa\)を選びました.だが,あなた方がこれから出会う問題は,「正解がわからない」「正解を出すのが自分の仕事」であるわけです.で・・・振動する解が誤りであると考えて,振動しなくなるまで粘性を入れる・・・というのが正しいのか?もしかすると,本当は振動するのが正解で,「いや,このまま実機を作ったら振動してヤバいっすよ」と設計部門に報告するべきであったところ,ファンデーションの厚塗りで振動しないように解を作り上げて,実機を作ると・・・墜落しますよね.
- 正解がわからないのに正解を出さねばならぬ.そのためには,さまざまな\(\Delta_x\)などのパラメータで解の傾向を調べ,「事実は,この方角にあるらしい」と推定する.それが一番重要です.
- 解の挙動を知っているから,そうやって解くという新解法も多い(未知の問題に対する挙動は不明ってわけだ). 騙されないようにしましょう.
さて,せっかく陰解法なのに\(\text{CFL}=0.8\)は小さいな?もっと大きくしてみましょう.すると
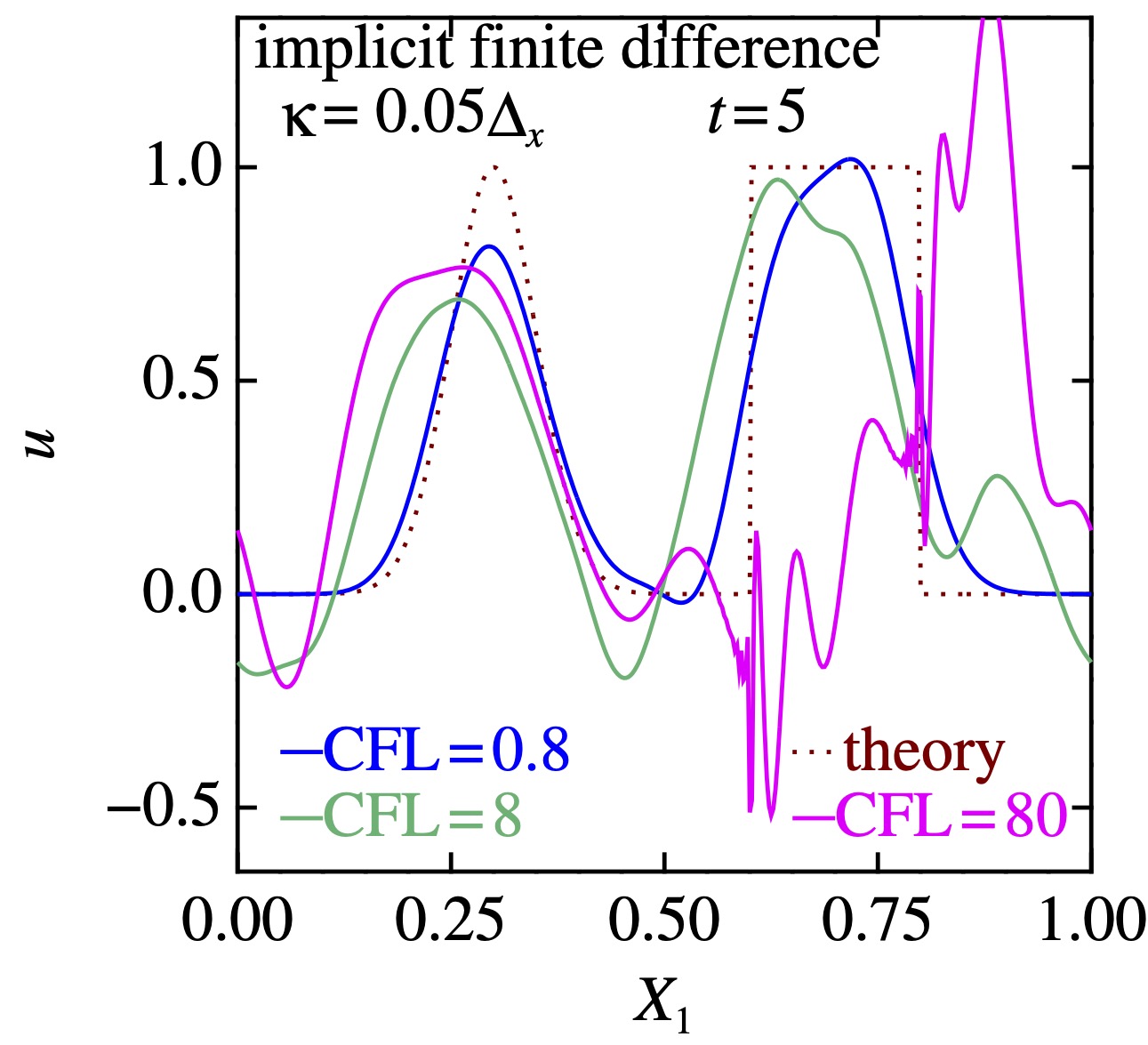
こうなってしまいます・・・陰解法は「CFLを大きくしても発散しない」んですが,「単に発散しないだけ. それ以上でも,それ以下でもない」なのです.今回のように,波が速度1で伝わる問題でCFLを大きくすると,\(\Delta_t\)由来の誤差が大きくなって,普通にうまくいきません.あれ?でも,この辺では,うまくいってたような?それは,そこでは定常解を求めたかったからですよ!
- 問題に応じて,適切な解析手法を選択するのは,あなたの責任である.
- 無敵なものって...ないと思う.
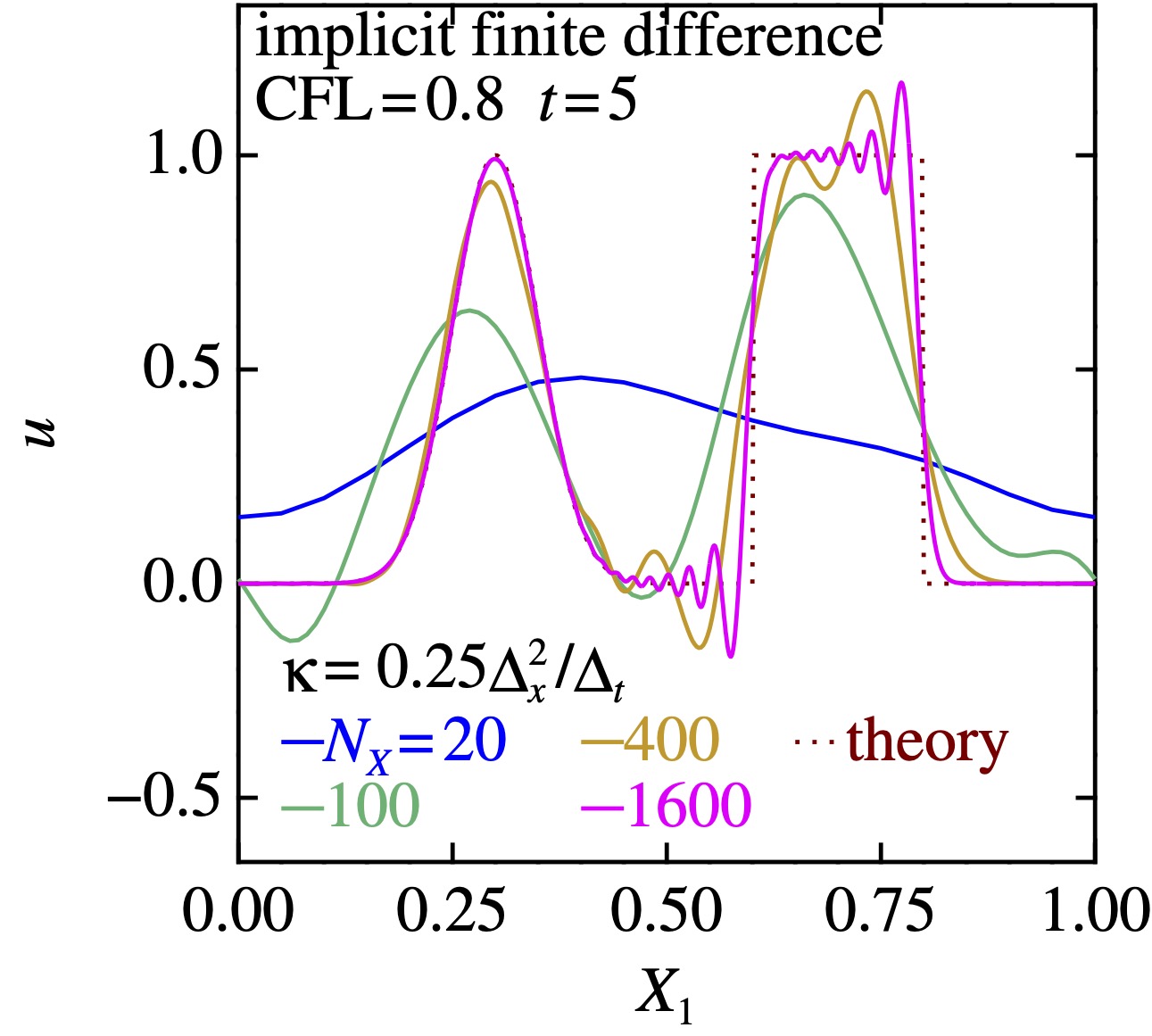
桜井法の結果も示しておこう. 人工粘性があれば,不連続を含むケースも, それらしい結果が得られる. あらかじめ正しい答えを知っている場合,それに合わせて\(\kappa\)を選ぶことはできそうである:
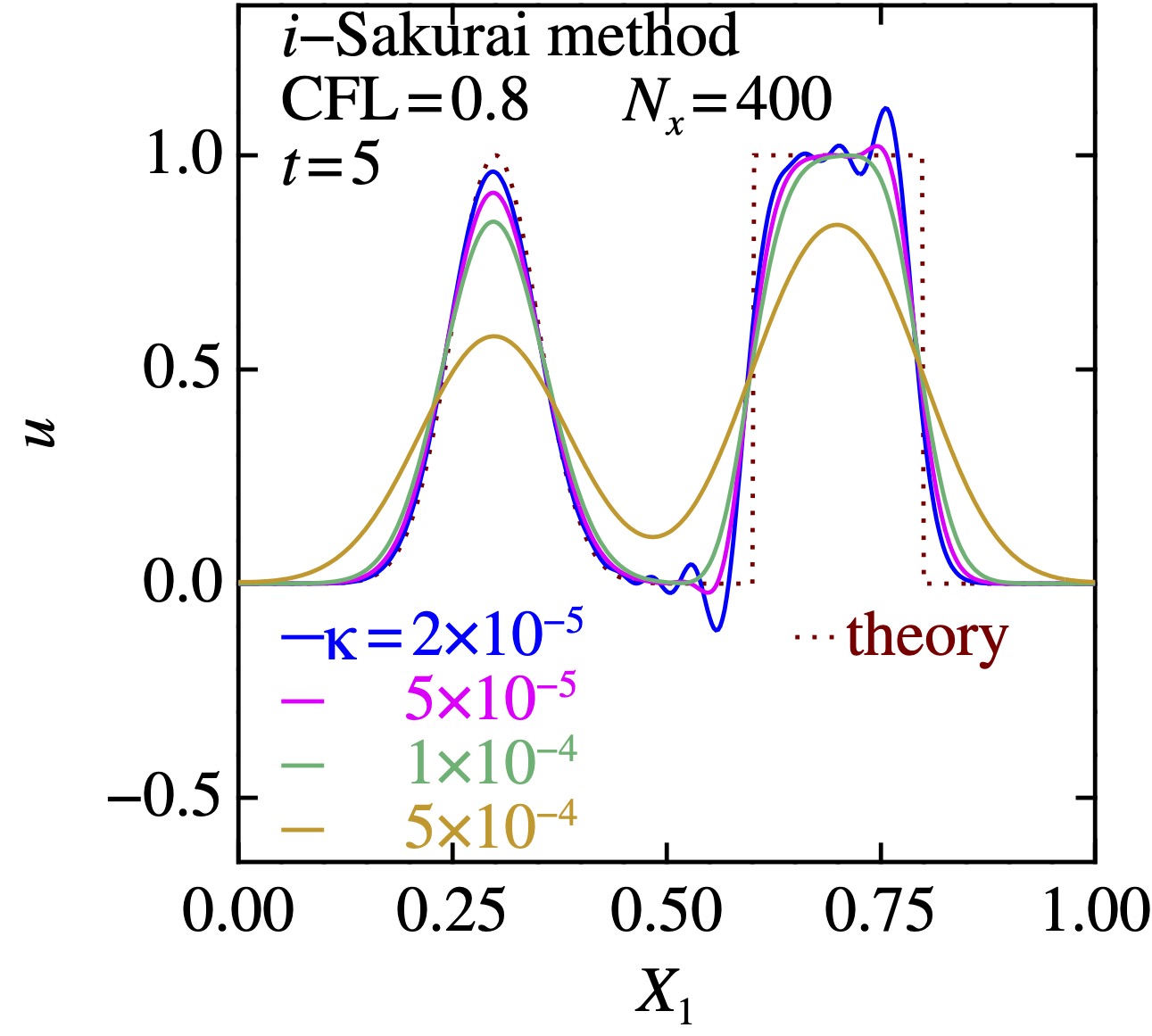 \(\kappa\)を変えてみた
\(\kappa\)を変えてみた  \(N\)を変えてみた
\(N\)を変えてみた
まあしかし,大体の場合,あなたの研究では上の赤字のところが成立しない(成立している場合,研究する価値がない)ので,なかなか大変であるよね.
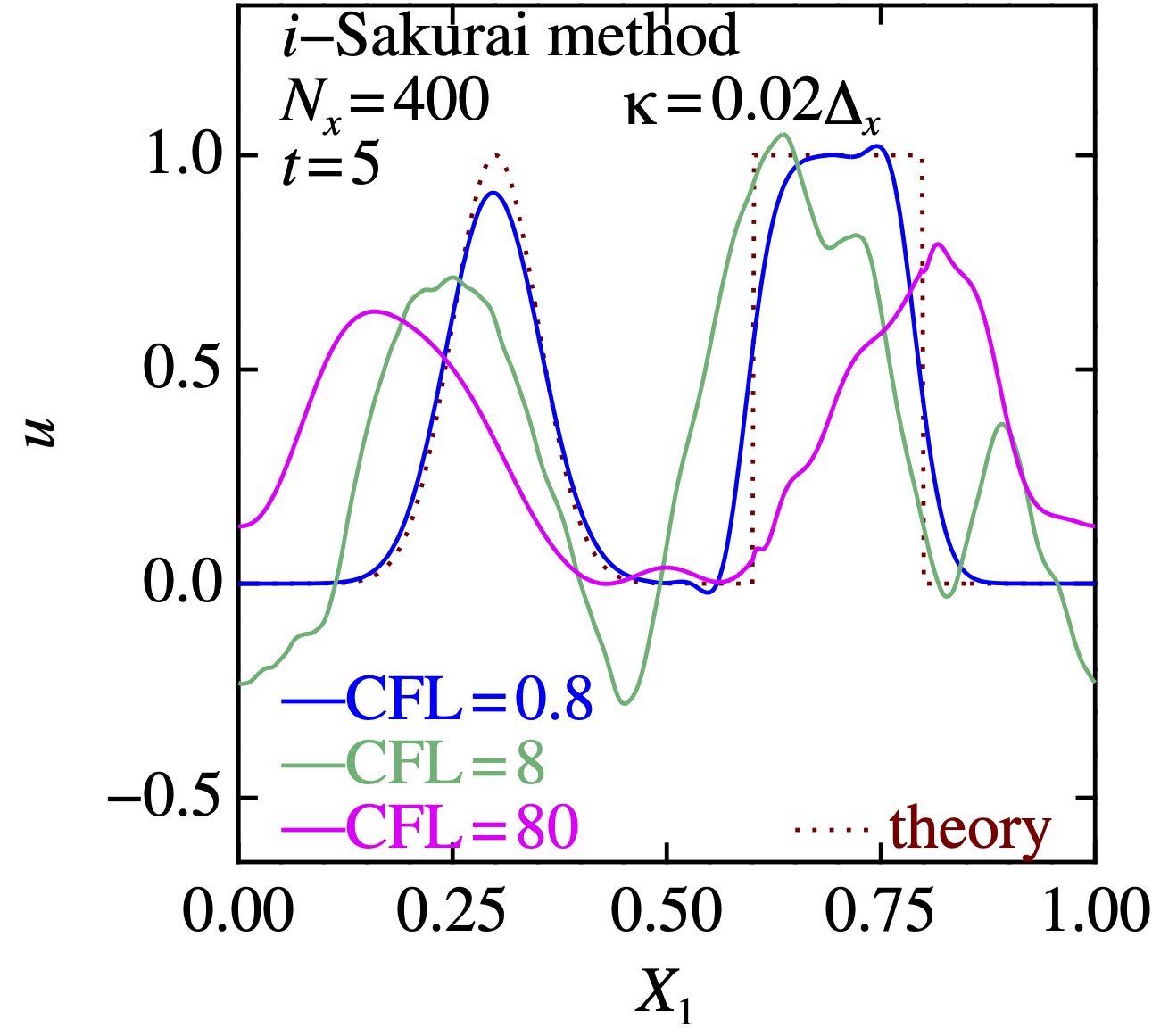 CFLを変えてみた
CFLを変えてみた
熱伝導方程式
2Dケース
二次元の熱伝導方程式\[\frac{\partial u}{\partial t}=\kappa\,\left(\dfrac{\partial^2 u}{\partial x^2}+\dfrac{\partial^2 u}{\partial y^2}\right)\]を解いてみましょう.
この場合,格子データとして\[u^{(n)}_{i,j}=u(n\Delta_t, i\Delta_x, j\Delta_x)\]が必要になります.時間ステップ\(n\)については周期性配列を使うとしても, 空間座標に\(i, j\)の2つのインデックスがあるところが1D問題とは異なります.
こういうのには「多次元配列」を使うのですが,これにはいろいろな方法があります.
多次元配列
2次元ならEigen
2次元までしか使えませんが, EigenのMatrixを利用するとA(i,j)というデータが使えますですね. お手軽で経験もあり,という訳ですが,3次元以上になると,困り始めます.
多次元配列は神への冒涜である派
そもそもコンピュータのメモリーは1次元的に「アドレス」に並んでいるものである. だから, u[i,j]のような多次元配列はマヤカシでありSyntaxSugarであり, 原理に対する許し難い冒涜と感じる原理主義者もいるでしょう.すると,自分で\(u(i_0,i_1,...i_N)\)をU[j]という1次元配列に並び替えて使えば良い!長所は計算がBoost並みに早いこと,短所は原理主義者は通常嫌われることです.とはいえ, 実戦でこれを理解していないと何かと不便なので, あとで自作を試みましょう.
Boost/Array
プログラミンゴでは「多次元配列」のように,誰もが使いたくなるような仕組みがあります.毎回自作するのは時間の無駄な気がします.で,偉い人たちがすでに作成したライブラリーと呼ばれるプログラムの塊が何種類かあります.Boostというのは,C++の有名なライブラリーで,とりあえずなんでもできることになっています.多次元配列も含まれていてBoost/Arrayを用いると,自作しなくても多次元配列が(原理的には)利用できます.長所は自分で書かなくても良いしBoostだから計算が早い,短所は!マニュアルを見なければ使い方がわからない,で,マニュアルを読んでも「?!?!」となるため,いつまでも使えるようにならないところです.
そこで,まずは,ライブラリーの利用方法を次の章で学びましょう.