配列データ

多次元配列クラスを自作

コンピュータは, そもそも自分のメモリーを1次元の数直線に並べて管理しています. ですので, 「多次元配列」というのは全て見せかけの虚構, 嘘で塗り固められた幻のようなものです．そう聞くと，「やはり本質を使わねばならん！」と叫び出す人が湧きます．では，その方法を学びましょう．

どうやって1次元配列を2次元配列に見せかけるのかというと：

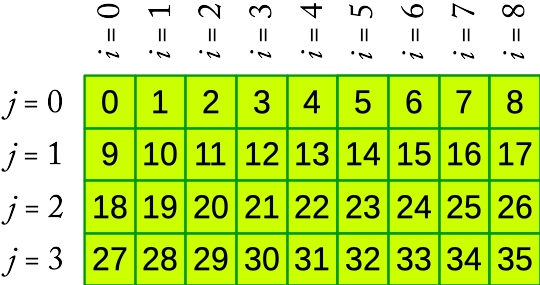
単純ですね．これで\([0:8]\times[0:3]\)の2次元配列ができます．1次元配列の範囲は\([0:36-1]=[0:35]\)です.

一般に, \([0:n-1]\times [0:m-1]\)の2次元配列であれば, 

• 要素数は\(n\times m\)
• \(k\)番目の要素は
  • \(i=k\%n\)  \(k\)を\(n\)で割った余りが, \(i\)
    • 例えば\(k=24\)ならば\(k\%9=6=i\)
  • \(j=k/n\)  \(k\)を\(n\)で割った結果が, \(j\)
    • 例えば\(k=24\)ならば\(k/9=2=j\)
• \((i,j)\)要素は\(i+n*j\)番目にある.
  • 例えば\((i,j)=(6,2)\)ならば\(k=6+9\times2=24\)

これを使って, 2次元配列を管理します．3次元以上の配列も, まったく同様です.

いちいち上の計算を書くのが面倒であれば, クラスにすればよい. これをプロが書いたものが, Boost/Array にあるので, 書くだけ無駄ですが,

• 機能が不足しているので改造しようとすると，困難に直面する．プロの書いたコードは，我々には意味不明だからである

まあ練習だと思って書いてみましょう. 設計としては

#include "../include/myArray.hpp"
...
myArray<double> A(10,12);    ←これで, double の10x12配列
myArray<SKit> B(10,10,20);　 ←これで. SKitクラスの10x10x20配列
...
A(4.5)=3.2;     ←こんなふうに使う
B(100,200,500)=SKit("initial.data");     ←添字がはみ出したらエラーして欲しい

くらいが要求でしょうか．書いてみましょう．

// myArray.hpp
#pragma once
#include <cassert>
#include <vector>
template <typename T>     ←テンプレートにしておけば，潰しがきく
class myArray
{
   std::vector<size_t> _sizes;     ←次元と寸法を記録しておこう
   std::vector<T> _data;           ←実際のデータはここに入れよう
public:
   // 一般の関数
   const size_t size() // myArray.size()でデータの総数
   const {
       size_t sz = 1;
       for (auto k : _sizes)
           sz *= k;
       return sz;
   }
   double *data() // myArray.data()で1次元配列のデータにアクセスできると便利である
   {
       return _data.data();
   }
   const double *data()　　　← const バージョンも作っておくと潰しがきく
   const {
       return _data.data();
   }
   double &operator[](const int k) // myArray[k]で1次元配列扱いをしよう. これでk番目のデータ
   {
       return _data[k];
   }
   const double &operator[](const int k)
   const {
       return _data[k];
   }
   auto begin() { return _data.begin(); }　　　←pvectorと同様の範囲指定for対策
   auto end() { return _data.end(); }
   const auto begin() const { return _data.begin(); }
   const auto end() const { return _data.end(); }
   auto &front() { return _data.front(); }
   auto &back() { return _data.back(); }
   const auto &front() const { return _data.front(); }
   const auto &back() const { return _data.back(); }
   // 1D配列
   myArray(const size_t n0) {resize(n0);}                                      // コンストラクタ0:(N)を呼び出す
   void resize(const size_t n0)
   {
       _sizes.resize(1); // 1次元配列にする
       _sizes[0] = n0;
       _data.resize(size());
   }
   const size_t serial(const int i0)
   const {
       assert(i0 >= 0);
       assert(i0 < _sizes[0]);
       return i0;
   }
   double &operator()(const int i0) // オペレータ0:(i)を呼び出す
   {
       assert(_sizes.size()==1);
       return _data[serial(i0)];
   }
   const double &operator()(const int i0) // オペレータ0:(i)を呼び出す
   const {
       assert(_sizes.size()==1);
       return _data[serial(i0)];
   }
   // 2D配列                          ←あとは，必要な次元を全部書いておけば良い
   myArray(const size_t n0, const size_t n1) {resize(n0,n1);}                   // コンストラクタ1:(N,M)を呼び出す
   void resize(const size_t n0, const size_t n1)
   {
       _sizes.resize(2); // 2次元配列にする
       _sizes[0] = n0;
       _sizes[1] = n1;
       _data.resize(size());
   }
   const size_t serial(const int i0, const int i1)
   const {
       assert(i1 >= 0);
       assert(i1 < _sizes[1]);
       return serial(i0) + _sizes[0] * i1;
   }
   double &operator()(const int i0, const int i1) // オペレータ1:(i,j)を呼び出す
   {
       assert(_sizes.size()==2);
       return _data[serial(i0, i1)];
   }
   double &operator()(const int i0, const int i1) // オペレータ1:(i,j)を呼び出す
   const {
       assert(_sizes.size()==2);
       return _data[serial(i0, i1)];
   }
   // 3次元配列
   myArray(const int n0, const int n1, const int n2){resize(n0,n1,n3);}      // コンストラクタ2:(N,M,O)を呼び出す
   void resize(const size_t n0, const size_t n1, const int n2){
       _sizes.resize(3); // 3次元配列にする
       _sizes[0] = n0;
       _sizes[1] = n1;
       _sizes[2] = n2;
       _data.resize(size());
   }
   const size_t serial(const int i0, const int i1, const int i2)
   const {
       assert(i2 >= 0);
       assert(i2 < _sizes[2]);
       return serial(i0, i1) + _sizes[0] * _sizes[1] * i2;
   }
   double &operator()(const int i0, const int i1, const int i2) // オペレータ2:(i,j,k)を呼び出す
   {
       assert(_sizes.size()==3);
       return _data[serial(i0, i1, i2)];
   }
   const double &operator()(const int i0, const int i1, const int i2) // オペレータ2:(i,j,k)を呼び出す
   const {
       assert(_sizes.size()==3);
       return _data[serial(i0, i1, i2)];
   }
};

コンストラクタを1次元用, 2次元用, 3次元用の3通りを用意してます．で，Debugビルドだと添字をチェック，Releaseビルドだと添字チェックなし，とする設定は，この辺です．

配列クラスが書けたら，テストしてみましょう．

自作の場合，機能拡張が容易です．例えば，添字を超えた範囲は，バーチャル配列にアクセスする，とかいうクラスを作ってみるのも良いでしょう．

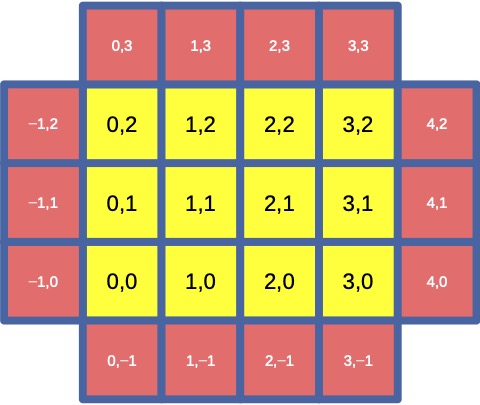　黄色のところの配列を定義すると，黙って赤色のところもついてくる，とかいう配列があったら結構便利だし