楕円型方程式
熱伝導方程式
2Dケース
になると, 拡散数条件\[D=\dfrac{\kappa\Delta_{t}}{\Delta_{x}^{2}}<\dfrac{1}{4}\]が厳しくて, 空間解像度が高い計算がしたいな,と思って, まあ最初は\(\Delta=0.01\)くらいか?と思ったら, 時間ステップが\(\delta<0.000025\), つまり\(t=5\)まで求めようとしたら, 20万ステップ必要になります. これでは計算に時間がかかりすぎるですね!これでは4K, 8Kレベルの解像度\(\Delta=0.0001\)とかは夢のまた夢,ってことになります.
そこで,陰的解法(インプリシット・スキーム)を採用しましょう. \[ u^{(n+1)}_{i,j} = u^{(n)}_{i,j} +\frac{\Delta_t}{\Delta_x^2}\left(u^{(n+1)}_{i-1,j}+u^{(n+1)}_{i+1,j}+u^{(n+1)}_{i,j-1}+u^{(n+1)}_{i,j+1}-4u^{(n+1)}_{i,j}\right)\]つまり\[u^{(n+1)}_{i,j}-\alpha\left(u^{(n+1)}_{i-1,j}+u^{(n+1)}_{i+1,j}+u^{(n+1)}_{i,j-1}+u^{(n+1)}_{i,j+1}\right) =\beta u^{(n)}_{i,j}, D=\frac{\Delta_t}{\Delta_x^2},\ \alpha=\frac{D}{1+4D},\ \beta=\frac{1}{1+4D}\]を解けば良い. なんかいっぱいあるので,関連する格子点を図で描くと

こんな感じになります.
- 注目している\((i,j)\)格子点を, 関連する\((i-1,j)\), \((i+1,j)\), \((i,j-1)\), \((i,j+1)\) が取り巻いている(囲碁だったら\((i,j)\)格子点が目のところになるやつ).
- んで,このスクラム組んでるやつを,様々な\((i,j)\)で考える.
- どこでも考えられるわけではなくて,赤格子点ではOKだが,緑格子点では,格子がはみ出してしまうので使えない・・・
- だが,緑格子点では,「境界条件」が使える.すると「格子点には,一個未知数がある」「格子点で使える式が一つある」ので,未知数の数=方程式の数になっており,解ける!
- ほんまか?4角の格子点を「スキップ」して考えたら,式の数は足りておる
- 例えば,\(x=0\)において\(u=1\)という境界条件があったとする.で,\(y=0\)において\(u=0\)という境界条件があったとする.
- すると\(x=0, y=0\)では, \(u=1\)なのか?\(u=0\)なのか?
- これは「特異点」というやつです.難しいので,とりあえず,今は4隅を考えないことにしましょう.
- というわけで,マス目のうち,四隅を除いた部分を解く!
さて, ここで\(u_{i,j}\)というのは, \(x\)方向に\(i\)番目, \(y\)方向に\(j\)番目のデータです.これは,どのようにプログラムしたら良いのでしょうか?
これを行列で書いてみましょう.
\[ \begin{bmatrix}1 & -\alpha & & -\alpha\\ -\alpha & 1 & -\alpha & & \ddots\\ & -\alpha & 1 & \ddots & & \ddots\\ -\alpha & & -\alpha & \ddots & \ddots & & \ddots\\ & \ddots & & \ddots & \ddots & \ddots & & \ddots\\ & & \ddots & & \ddots & \ddots & \ddots & & \ddots\\ & & & \ddots & & \ddots & \ddots & \ddots & & \ddots\\ & & & & {\color{purple}{-\alpha}} & & {\color{magenta}{-\alpha}} & {\color{cyan}1} & {\color{orange}{-\alpha}} & & {\color{teal}{-\alpha}}\\ & & & & & \ddots & & -\alpha & \ddots & -\alpha & & \ddots\\ & & & & & & \ddots & & & \ddots & -\alpha & & -\alpha\\ & & & & & & & \ddots & & \ddots & \ddots & \ddots\\ & & & & & & & & \ddots & & \ddots & \ddots & -\alpha\\ & & & & & & & & & -\alpha & & -\alpha & 1 \end{bmatrix}
\begin{bmatrix}u_{1,1}^{(n+1)}\\ \vdots\\ \vdots\\ \vdots\\ {\color{purple}{u_{i-1,j}^{(n+1)}}}\\ \vdots\\ {\color{magenta}{u_{i,j-1}^{(n+1)}}}\\ {\color{cyan}{u_{i,j}^{(n+1)}}}\\ {\color{orange}{u_{i,j+1}^{(n+1)}}}\\ \vdots\\ {\color{teal}{u_{i+1,j}^{(n+1)}}}\\ \vdots\\ u_{N-1,N-1}^{(n+1)} \end{bmatrix} \]
\[=
\begin{bmatrix}u_{1,1}^{(n)}\\ \vdots\\ \vdots\\ \vdots\\ {\color{purple}{\beta u_{i-1,j}^{(n)}}}\\ \vdots\\ \color{magenta}{\beta u^{(n)}_{i,j-1}}\\ {\color{cyan}{\beta u_{i,j}^{(n)}}}\\ {\color{orange}{\beta u_{i,j+1}}}\\ \vdots\\ {\color{teal}{\beta u_{i+1,j}^{(n)}}}\\ \vdots\\ u_{N-1,N-1}^{(n)} \end{bmatrix}
+
\begin{bmatrix}+\alpha u_{0,1}+\alpha_{1,0}\\ +\alpha u_{0,2}\\ \vdots\\ \vdots\\ 0\\ \vdots\\ \vdots\\ \vdots\\ 0\\ +\alpha u_{0,N-1}+\alpha u_{1,,N}\\ \vdots\\ \vdots\\ +\alpha u_{N-2,N-1}+\alpha u_{N-1,N-2} \end{bmatrix} \]
非斉次項は, 前時間ステップの値と, 境界条件の値から構成されているので注意.
あとは,これを解けば良い.Eigen/Sparseを使えば簡単ですね!
\(\Delta=0.01\)でもノートPCでなんとか実行できます.\(\delta=0.1\)でも発散しないけど, ビデオをきれいに撮るために\(\delta=0.001\)で実行したのが下のやつです.
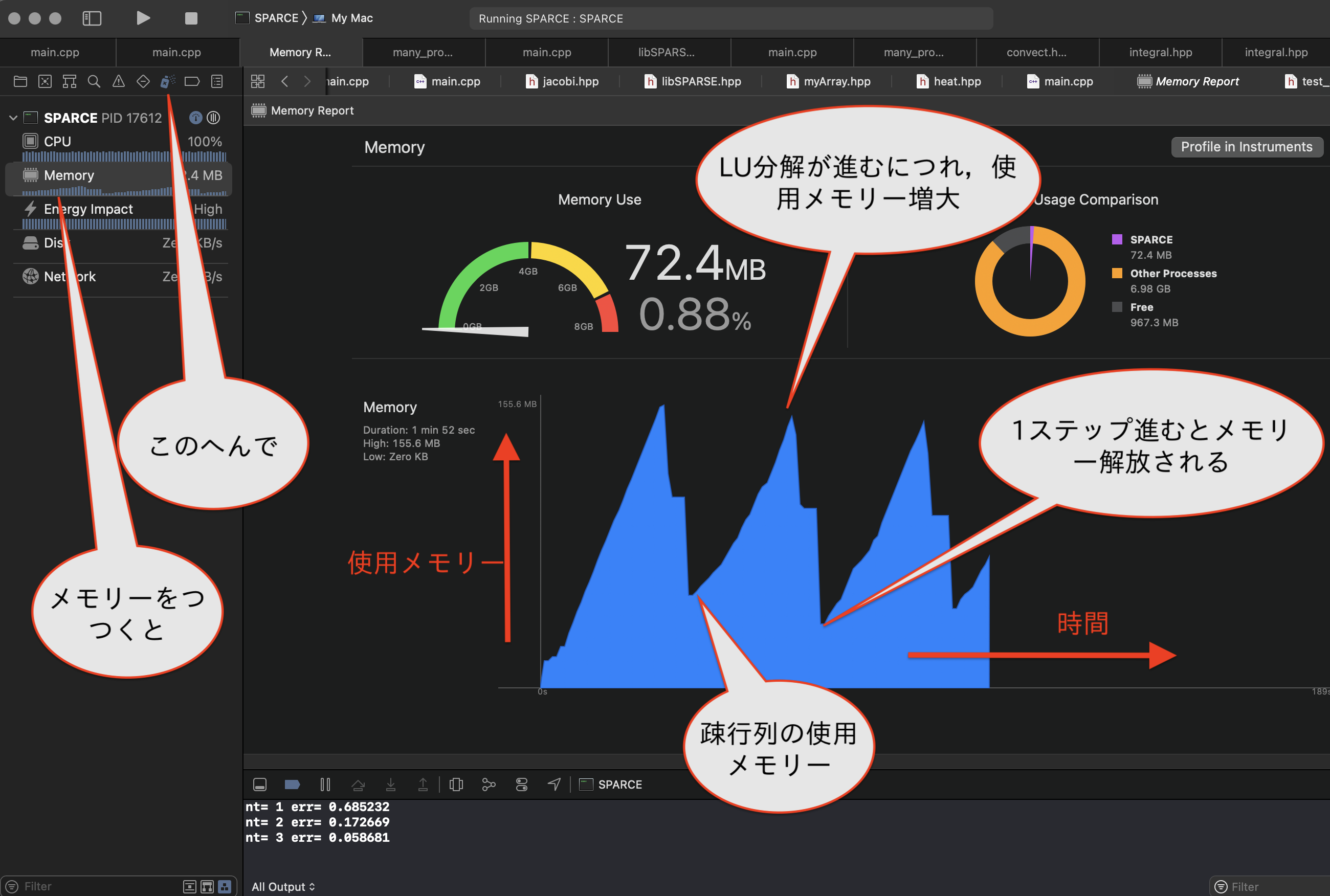
XCodeで実行中に使用メモリーサイズを調べると,LU分解している時に使用メモリーが微妙に爆発していることがわかります.どれくらい爆発するかは,問題によって異なるでしょう.このケースでlibSPARSEであると,数倍に増えるみたいですね.
インプリシットスキームは\(\delta\to\infty\)でも発散しないので,極限をとってみましょう. すると\[4u^{(n+1)}_{i,j}-\left(u^{(n+1)}_{i-1,j}+u^{(n+1)}_{i+1,j}+u^{(n+1)}_{i,j-1}+u^{(n+1)}_{i,j+1}\right) =0\]になって, 定常のLaplace方程式を解いていることになります.
set(CMAKE_C_STANDARD_REQUIRED ON) -- Found PkgConfig: /usr/local/bin/pkg-config (found version "0.29.1") -- Found GSL: /usr/local/include (found version