ここに説明があるので，ここではHowTo的に描いてみる．

インストール

まずはMATLABあるいはOctaveをインストールする．起動すると, こんな感じだ：

oct

ファイル形式

読み込めるファイルは, 次のようなものである:

X座標  Y座標  関数値1 関数値2 ....

で, 複数行書く時には, Y座標を変更していき, 次にX座標を変更させた方が手数が少なくて済む．

ソフトウェア操作

起動してフォルダーを選択し, ファイルを読み込む. 例えば my.data が

まあこの場合は\(u(x,y)=1+y^2\)ということである．この場合

>> A=load("my.data")
>> x=A(:,1)  #これで1列目がxベクトル
>> y=A(:,2)  #これで2列目がxベクトル
>> u=A(:,3)  #これで3列目がuベクトル

いやいや, それらは2次元データなので reshape するわけね．

>> x=reshape(x,3,2)  #y方向に3格子, x方向に2格子
x =0   1
   0   1
   0   1
>> y=reshape(y,3,2)
y =0   0
   1   1
   2   2
>> u=reshape(u,3,2)
u =1   1
   2   2
   5   5

なるほど. では描いてみる:

>> contour(x,y,u,10)

デフォルトでは, かな〜りダサい図を描く：

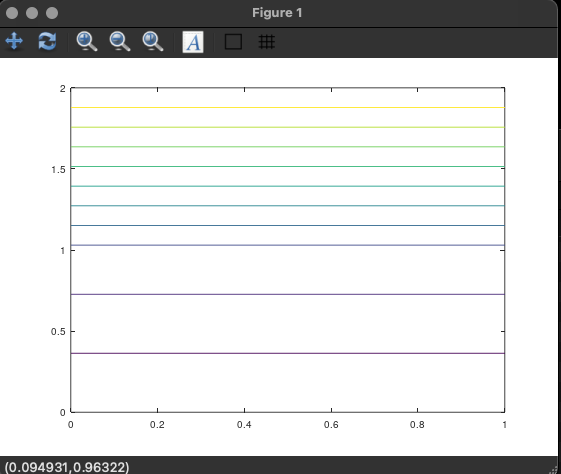
ツッコミどころ満載である：

文字がダサい．まるでコンピュータが描きそうな字だ．Timesくらい使えよ
- set(gca, "FontName", "Times New Roman");
文字が小さい．講義室の後ろで「みえませーん」叛乱が起こる
- set(gca,'fontsize',20) で訂正可能
線が細い．
線のラベルがないので関数値が不明
- contour(x,y,u,10,'ShowText','on')で一応つくが, 使い物にはならない
XとYのスケールが異なる
- pbaspect([1 1 1])で訂正可能

いろいろいじるのが面倒である．その場合には, 保存して別のソフトで描くことも可能である.

いつも使っているのはこれ：

function [val lev] = savecontour(filename,cnt)
fid=fopen(filename,'w');
npar = 0; ptr = 0; N = size(cnt,2);
while(ptr < N)
  npar++; ptr++;
  lev{npar} = cnt(1,ptr);
  n = cnt(2,ptr);
  val{npar} = cnt(:,((ptr+1):(ptr+n)))';
  for i=1:n
    fprintf(fid,"%f %f\n",cnt(1,ptr+i),cnt(2,ptr+i));
  end
  fprintf(fid,"\n");
  ptr+=n;
  endwhile;
  fclose(fid);
endfunction;

これで

[ cnt lev ]=contourc(x,y,u);
savecontour("mycont.dat",cnt)

こうすると mycont.dat に X Y座標が保存されるので, あとは好きなように描けば良い. たとえば

graph -Tps -C -x 0 1 -y 0 2 -nx -ny --line-width 0.0025 --frame-lin\
e-width 0.002 mycont.dat |ps2pdf -dEPSCrop - new.pdf

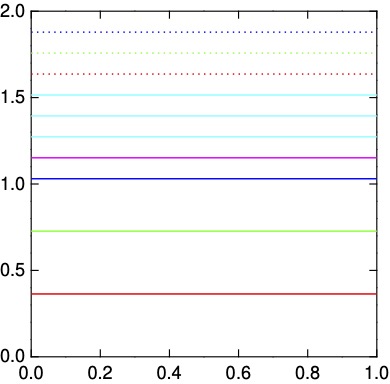
これでPDFファイルをゲットだ:

解を保存

収束後の解を保存しよう. 例えばデータを保存するC++コードは

#include <boost/filesystem.hpp>
...
std::ofstream ofs;
...
boost::filesystem::path folder=getenv("HOME");
boost::filesystem::current_path(folder/"tes_test");
ofs.open(filename);
...
void write()
{
  for(int i=0;i<U.size(0);i++) for(int j=0;j<U.size(1);j++)
    ofs  << static_cast<double>(i)/(U.size(0)-1) << " "
         << static_cast<double>(j)/(U.size(1)-1) << " "
         << U(i,j) <<std::endl;
}

こんな感じである. サンプルの図は100x100格子で計算したが, 収束が遅く, 前回とのずれが\(10^{-10}\)に達するまでに約30000イタレーションを要した.

こいつを作図するOctaveコードを, jacobi.m ファイルに作成した:

clear;
function [val lev] = savecontour(filename,cnt)
fid=fopen(filename,'w');
npar = 0; ptr = 0; N = size(cnt,2);
while(ptr < N)
  npar++; ptr++;
  lev{npar} = cnt(1,ptr);
  n = cnt(2,ptr);
  val{npar} = cnt(:,((ptr+1):(ptr+n)))';
  for i=1:n
    fprintf(fid,"%f %f\n",cnt(1,ptr+i),cnt(2,ptr+i));
  end;
  fprintf(fid,"\n");
  ptr+=n;
endwhile;
fclose(fid);
endfunction;
#-------------
A=load("../jacobi_100.dat");//あんたがC++で作成したデータファイルを指定
nx=101;
ny=101;
x=A(:,1);
y=A(:,2);
u=A(:,3);
x=reshape(x,ny,nx);
y=reshape(y,ny,nx);
u=reshape(u,ny,nx);
[ cnt lev ]=contourc(x,y,u,7);
[ val lev ]=savecontour("contour_100.dat",cnt);//等高線をcontour_100.datに保存

作成したコードは, Octave画面で次のように実行できる:

>> run  jacobi.m

これで contour_100.dat ができたので, 作図した:

graph -Tps -C -x 0 1 -y 0 1 -nx -ny -X '\fIx' -Y '\fIy'\
   --label-font-name Times-Italic --font-size 0.055\
   --frame-line-width 0.0025 --line-width 0.0025\
   contour_100.dat |ps2pdf -dEPSCrop - contour_100.pdf

これで contour_100.pdf が完成する．ここまで graph コマンドが長いと, draw.sh の利用を検討した方がいいかもしれない.

MATLAB/OCTAVE

インストール

ファイル形式

ソフトウェア操作

解を保存